Current-Based Impedance Control for Mobile Manipulators Without Force/Torque Sensors

Summary

As robots transition from industrial settings to human-centered spaces, integrating mobile manipulation and compliant control becomes vital for efficient and safe task execution. Mobile manipulation extends the robot's workspace by combining navigation and manipulation capabilities, enhancing flexibility and efficiency. Moreover, compliance is mandatory for robust behaviors in unstructured environments and safe operation in the proximity of humans. Compliance is commonly achieved through indirect force control methods such as admittance and impedance control. However, these methods require contact information that are typically derived from measurements of the joint torques or from a force/torque sensor mounted at the end-effector. Such equipment can be expensive, and off-the-shelf robots might not come equipped with them. Further challenges arise based on the control mode supported by the robot. For instance, while admittance control can be applied to position/velocity-controlled robots, compliance is only achieved concerning the measured forces. On the other hand, impedance control is exclusive to torque-controlled robots, yet it effectively achieves compliance to all forces interacting with the robot. Therefore, implementing compliant control on a mobile manipulator poses significant challenges. This work presents a holistic approach to address compliance for mobile manipulators using off-the-shelf current-controlled manipulators and velocity-controlled mobile bases without adding force/torque sensors. In the context of the manipulator, the approach involves leveraging the direct correlation between the actuator current and the resulting joint torque, overcoming the typical reliance of impedance control on torque sensors. Additionally, we present two operational modes to achieve a compliant mobile-manipulator. First, a guidance mode facilitating compliant lead-through interaction between the manipulator and the mobile base. Second, a tracking mode which involves the base following the arm, enhancing stability and extending the workspace.

Calibration Method

We consider a mobile manipulator, including a current-controlled manipulator without force/torque sensors, which does not allow the direct application of an impedance controller. Thus, the goal is to derive the relation

that matches the actuator currents $\boldsymbol{c}$ with the joint torques from the impedance controller $\boldsymbol{\tau}$. This process utilizes the robot's model and Earth's gravity to estimate the ratio between the actuator current and the resulting torque. Additionally, it estimates joint friction and incorporates a compensatory control strategy. Challenges arising from model inaccuracies and their resolution are addressed. To enhance clarity, we outline the process for a single joint below but note that this can be replicated for each joint.

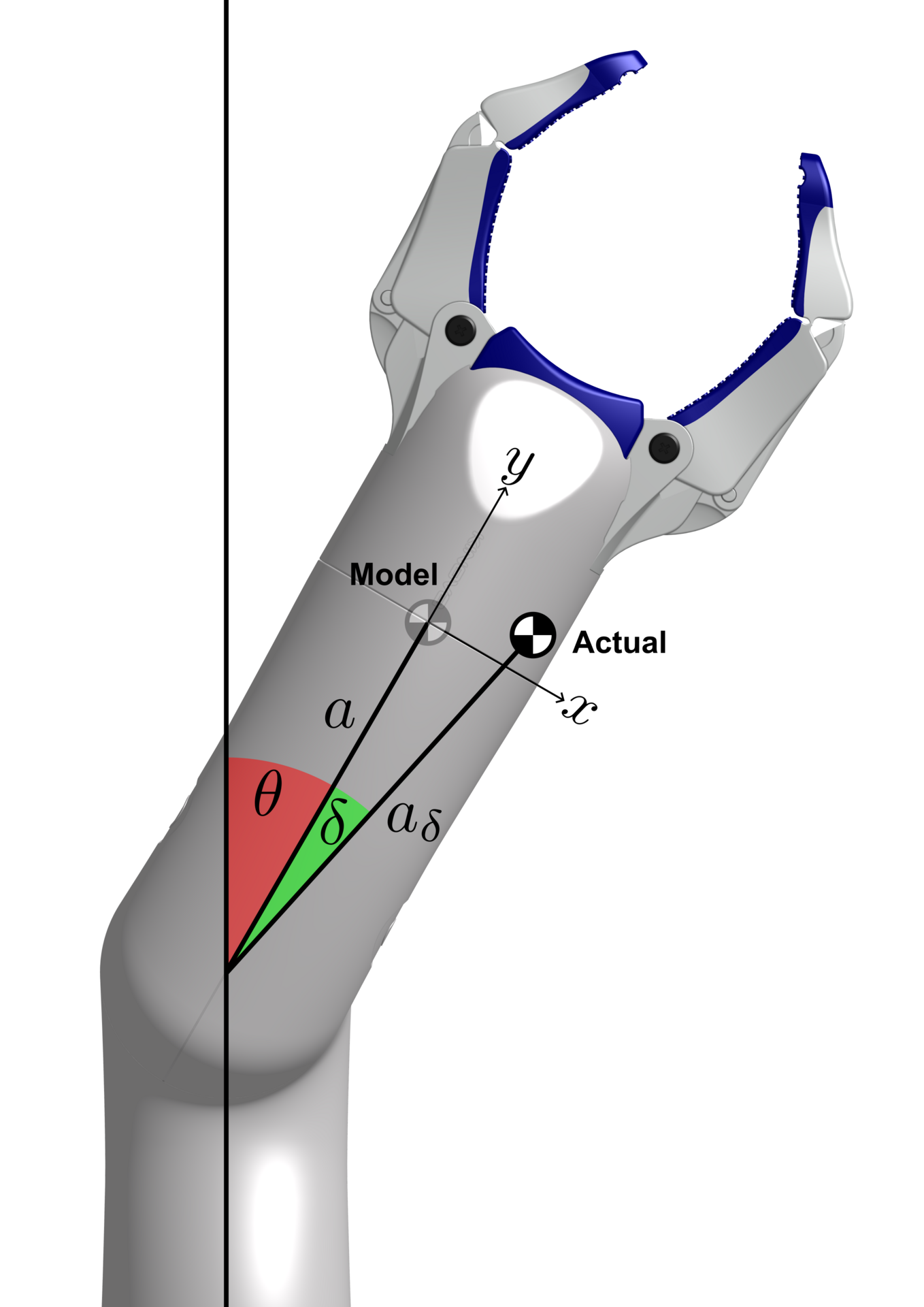
We start by estimating the ratio $r$ between the actuator current $c$ and the model-based actuator torque $\tau$ so that the relation above becomes $c = r \tau$ for a single joint. Initially, we assume zero friction, but friction is addressed later. For any given robot pose, it is possible to calculate the gravitational torque $\tau_\mathrm{g}$ acting on the joint. For a constant rotational velocity of the robot, $\tau$ is exactly the opposite of $\tau_\mathrm{g}$, which depends on the mass $m$ the joint is carrying, the gravity constant $g$, the length of the moment arm $a$, and the angle between the moment arm and the direction of gravity $\theta$. Given these information about the model and current data recorded when moving the joint with a constant velocity, the ratio $r$ can be estimated. In a similar way, the friction loss $l$ can be estimated resulting in $c=r \tau +l$. How the controller can be adapted to compensate for the estimated friction loss is described in detail in the thesis.

The approach described for deriving the ratio $r$ and friction loss $l$ relies entirely on the accuracy of the robot's model. However, inaccuracies in the model, e.g. the center of mass location (COM), can occur. More information on how the presented calibration method can account for model errors is described in the thesis.

Guidance and Tracking Mode

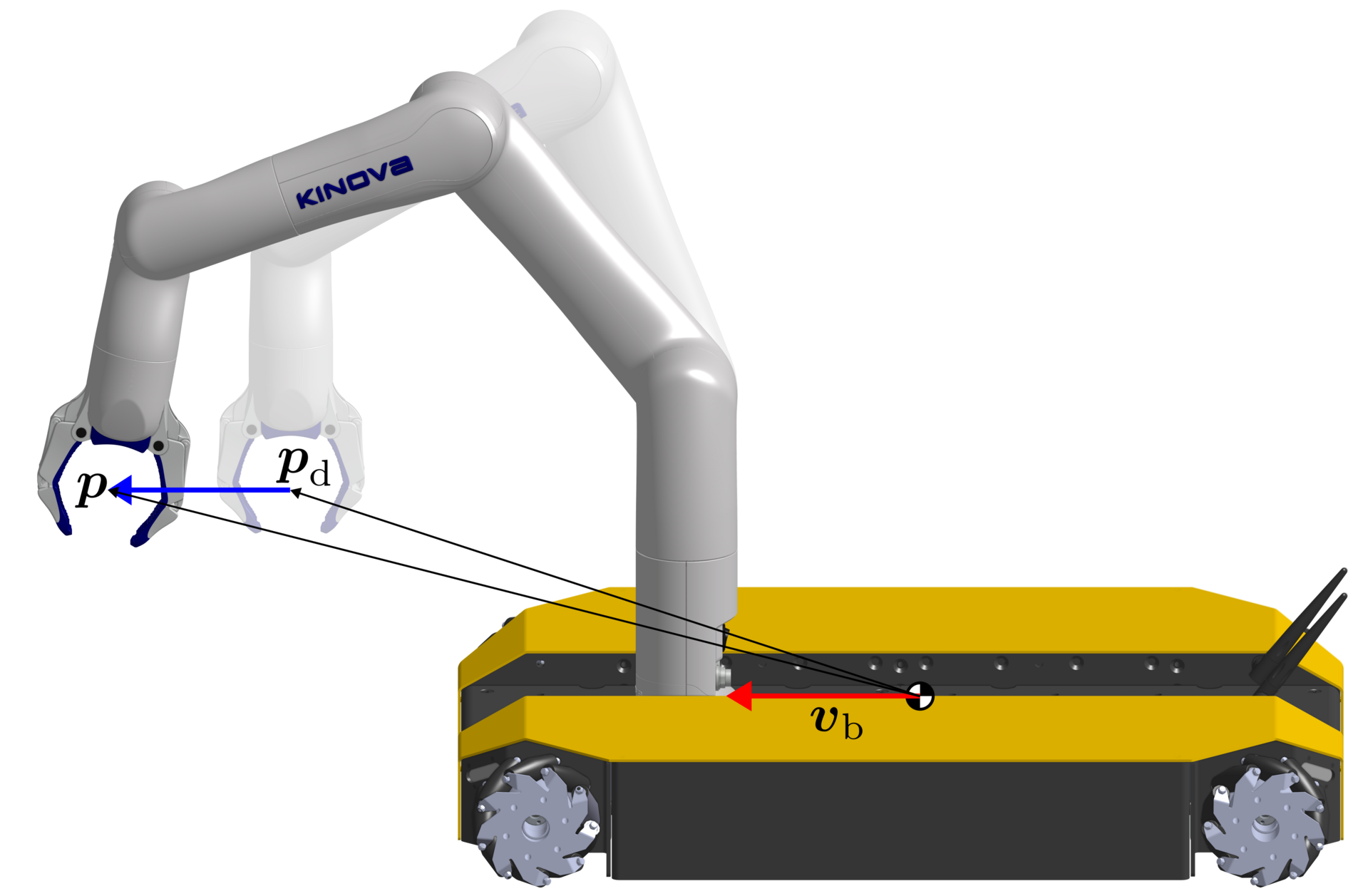
We have introduced a calibration method that allows impedance control on a current-controlled manipulator without force/torque sensors. Implementing impedance control on many off-the-shelf mobile bases is not possible since they only allow position/velocity control. This is also the case for the considered mobile base. Hence, an alternative control strategy is employed for the base, where the base controller aims to keep the end-effector position $\boldsymbol{p}$ always at a defined desired position $\boldsymbol{p}_\mathrm{d}$, both expressed in the reference frame of the base itself as shown in the left image below. A difference between $\boldsymbol{p}$ and $\boldsymbol{p}_\mathrm{d}$ results in a base velocity using a defined constant gain. With this controller, the base will always follow the end-effector when the end-effector deviates from the desired position.

We present two operational modes for interacting with the mobile manipulator: A guidance mode to guide the mobile manipulator around the workspace through interacting with the arm, and a tracking mode to execute a tracking task. Both modes are compliant in the case of contacts.

In the guidance mode, the target of the end effector is statically placed in the reference frame of the base, see center image above. By defining $\boldsymbol{p}_\mathrm{d}$ at the same location, the base will not move when the end-effector reaches the target. When the user pushes the end-effector away, the base will follow. Since the target is statically placed in the reference frame of the base, the target follows the movement of the base. When the end-effector is released, it can return to the target, and the base stops. This setup allows the user to easily move the mobile manipulator by leading it through interaction with the arm.

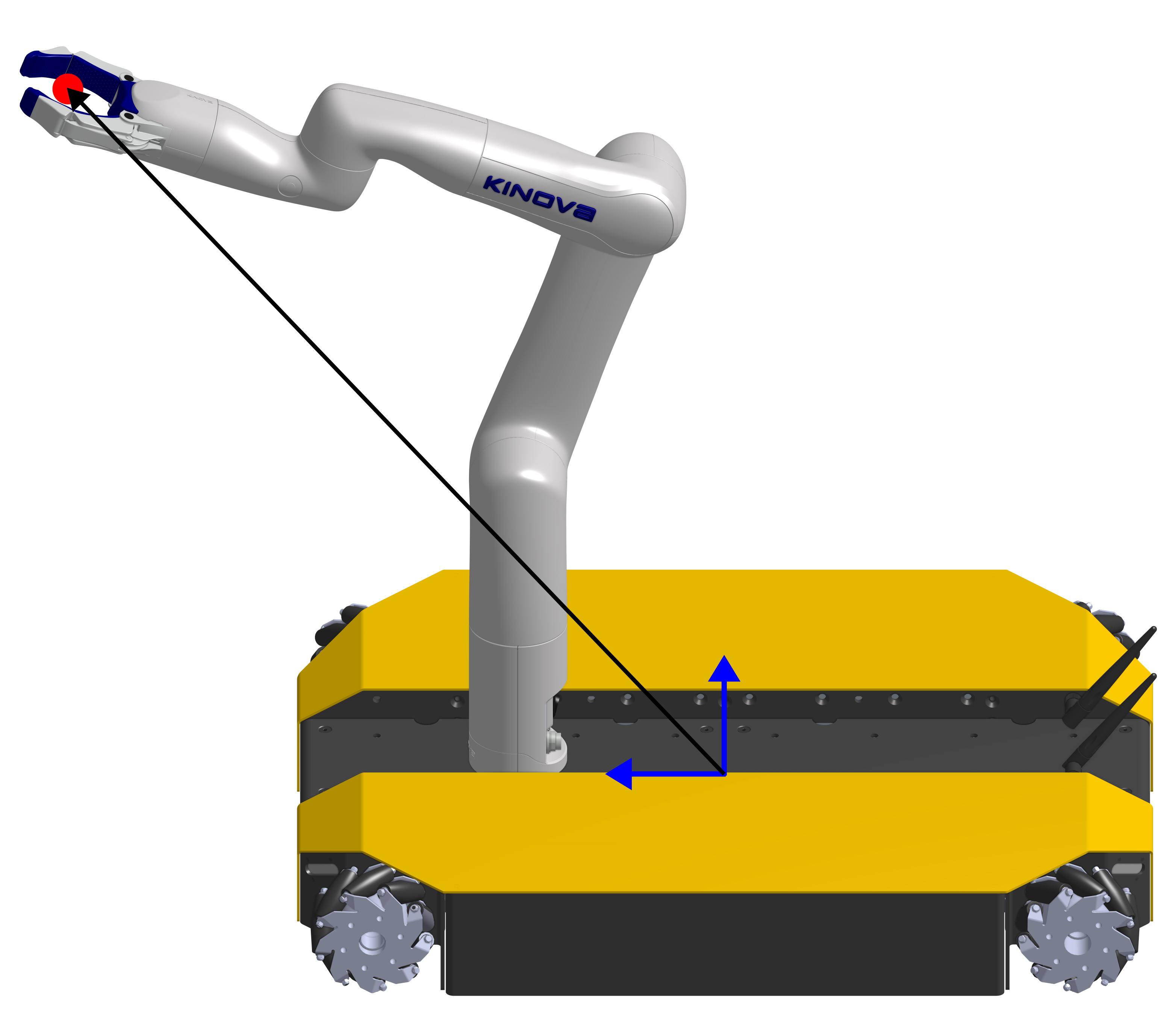
In tracking mode, the target is placed in the reference frame of the world, see right image above. Therefore, the target does not follow the movement of the base, in contrast to the guidance mode. The user can push or pull the end-effector away from the target, resulting in a movement of the base following the end-effector. Since the target is defined in the reference frame of the world, the robot moves further away from the target as long as the user keeps pushing the robot away. When the robot is released, the end-effector tries to get back to the target. The base will move, following the end-effector, until the end-effector is at the desired position $\boldsymbol{p}_\mathrm{d}$ relative to the base.

Conclusions

This thesis presented a holistic approach to addressing compliance for mobile manipulators using off-the-shelf manipulators and wheeled mobile bases. Specifically, we introduced a calibration method that enables the application of impedance control on current-controlled manipulators. This method involves estimating the torque/actuator current ratio and friction loss and can account for model inaccuracies using only signals available from standard position control. Thus, no force/torque sensors are required. Furthermore, we presented two operational modes for interacting with the mobile manipulator that allow a human to guide the robot through interaction with the manipulator and extend the manipulator's workspace. We showed the consistency of the calibration method in real-world experiments and we evaluated our impedance controller, which considers the identified torque/actuator current ratio and friction loss on a manipulator. Additionally, we showcased the whole-body implementation on a mobile manipulator consisting of off-the-shelf components without relying on any force/torque sensors and showed that compliant control on a current-controlled robot without force/torque sensors is possible with good performance.