Simultaneous Synthesis and Verification of Neural Control Barrier Functions through Branch-and-Bound Verification-in-the-loop Training

Neural Control Barrier Function Training and Verification

The primary goal of this thesis is to train a neural network (NN) $\hat{h}_w(x)$ until it satisfies the CBF conditions (see paper or thesis) and renders a large forward invariant set. We present a new empirical loss design based on the time-dependent Control Barrier Value Function Variational Inequality which we extended to the infinite- horizon.

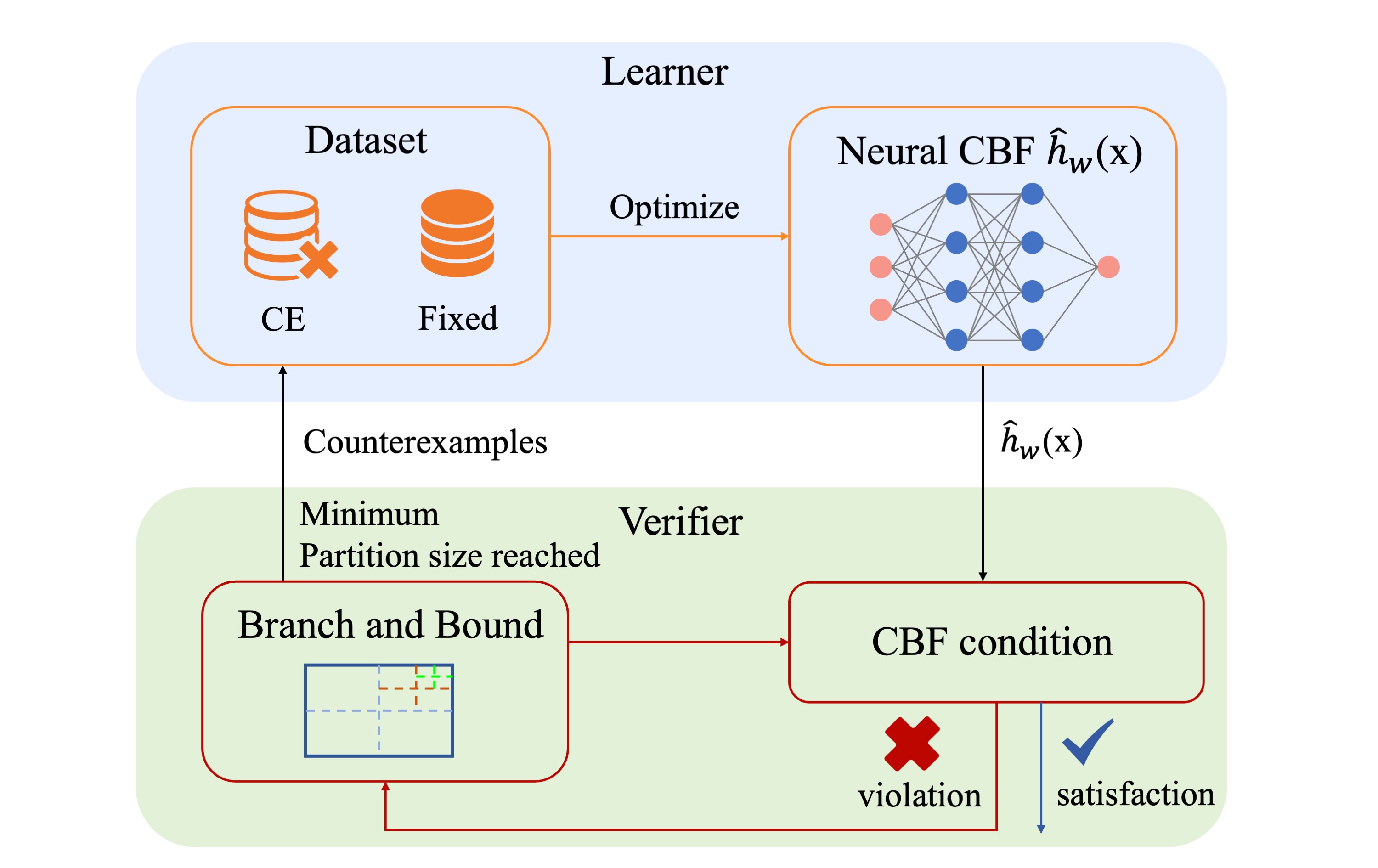
Since the NN is trained on finite data points, one must note that the NN may not satisfy the CBF conditions everywhere in the state space, even if the empirical loss decreases to zero. In fact, they may be violated almost everywhere, which means the NN may fail to render a forward invariant set and the safety guarantee no longer exists. We leverage bound propagation techniques, i.e. CROWN, and the Branch-and-Bound scheme (BBS) to efficiently verify nCBFs. In particular, we partition the state space and utilize linear bound propagation techniques to provide lower and upper bounds of the NN and its Jacobian. These bounds are used to verify if the NN satisfies the conditions to be a CBF. The BBS is applied to refine the partition to improve scalability and achieve less conservative bounds. We refer to the above verification scheme as Branch-and-Bound Verification scheme (BBV). To accelerate training, we embed the BBV into the training loop to synthesize and verify an nCBF simultaneously, which we refer to as Branch-and-Bound Verification in-the-Loop Training (BBVT). We start with the initial fixed training dataset D that contains a number of uniformly sampled points. During the training procedure, we optimize the NN to decrease the loss. We apply BBV until the minimum partition size is reached. The hyperrectangles for which the computed bounds do not satisfy the CBF conditions are treated as the violation areas. Their center points are added to the Counterexample (CE) dataset and the training procedure is repeated until the BBV returns satisfaction or the maximum number of iterations is reached. See the Figure above for an overview of the BBVT.

Results

We evaluate our proposed framework on two systems: an inverted pendulum and a 2D navigation task. We provide a comprehensive assessment on the inverted pendulum with an inadmissible area, addressing the verification efficiency and the size of the safe set, respectively. Furthermore, we consider a 2D navigation task with nonconvex constraints to display the practical use of our framework and combine the nCBF with reinforcement learning (RL) to achieve safe policy learning.

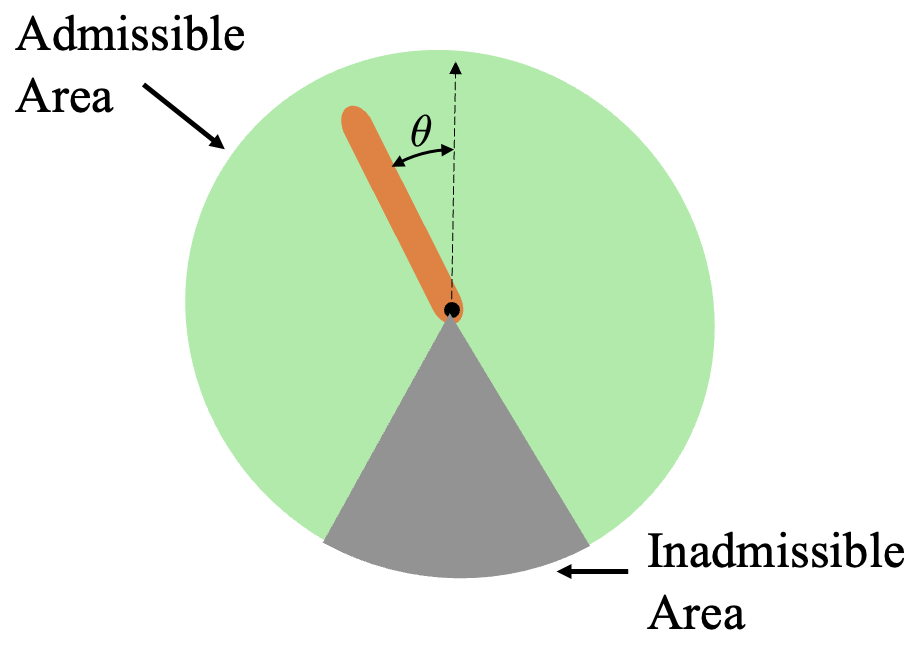
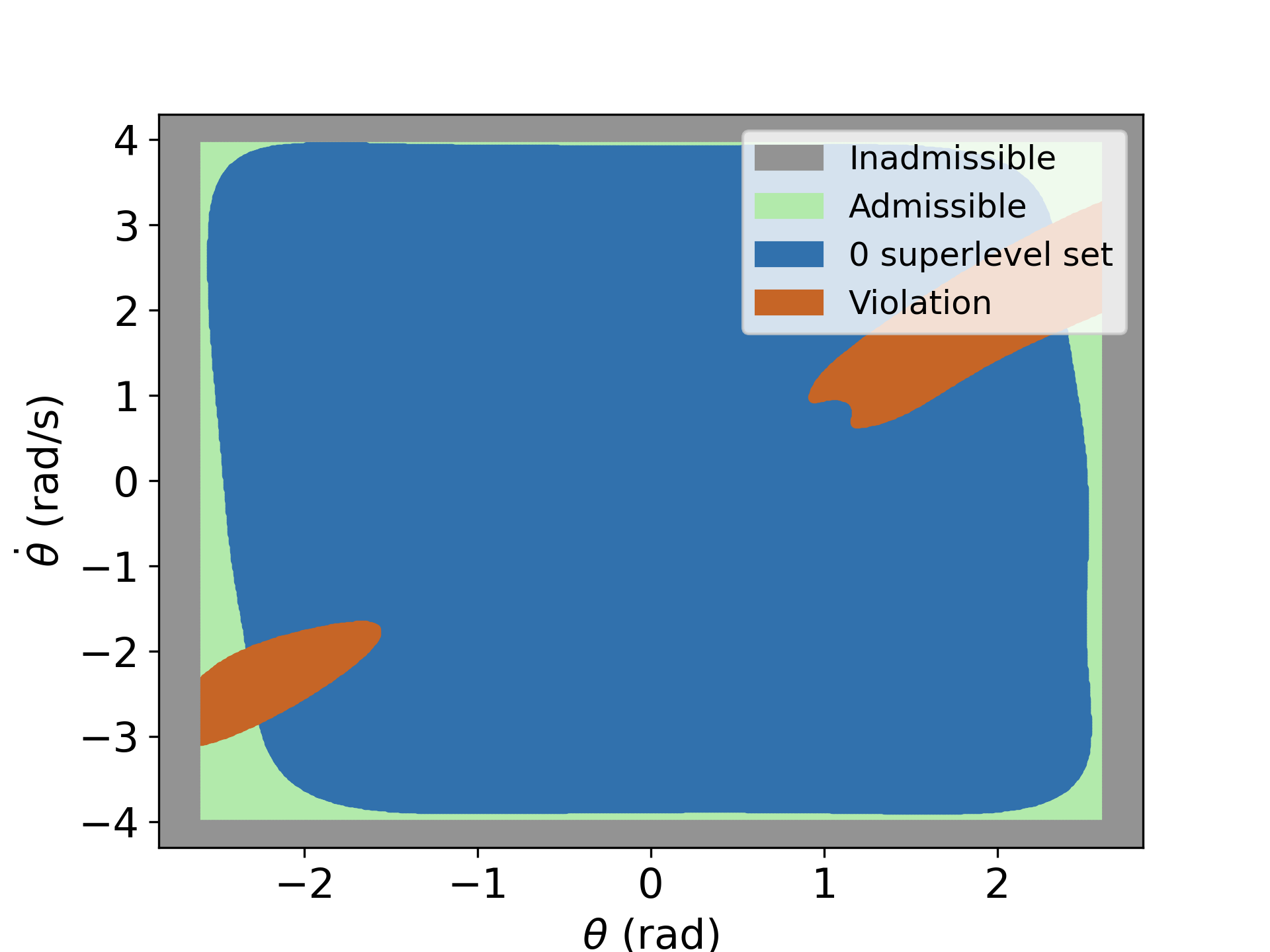
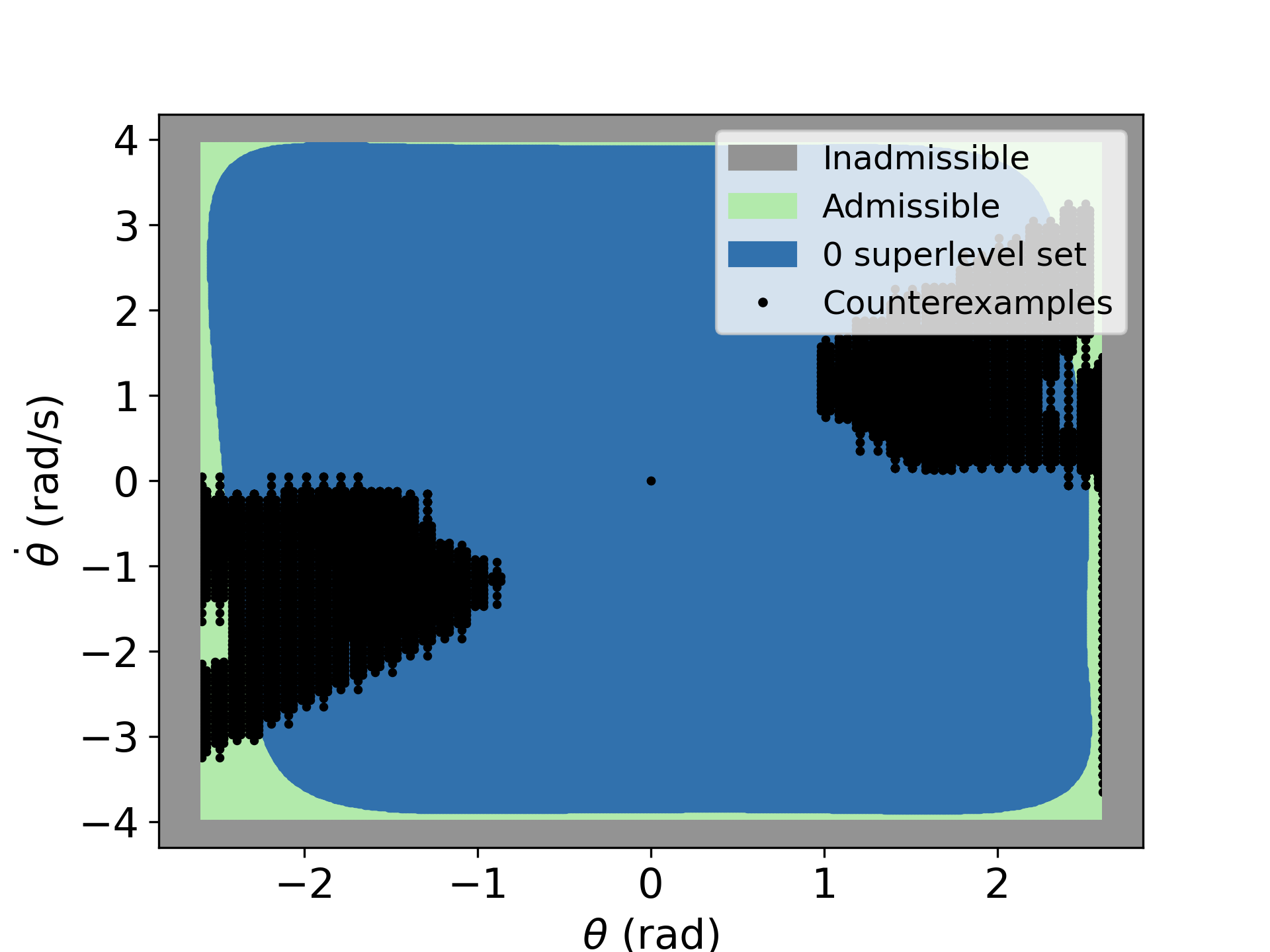
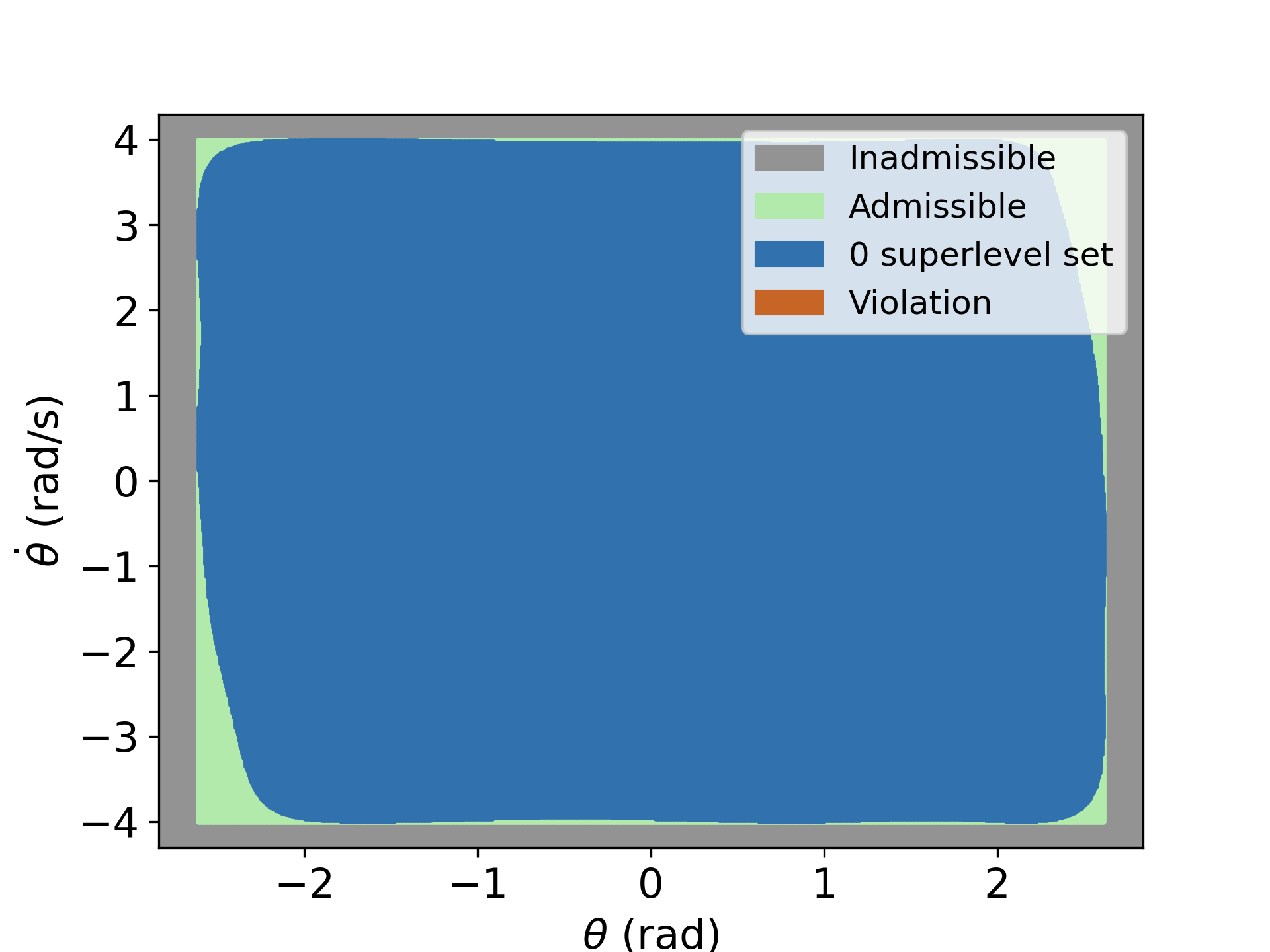
To showcase the disadvantage of training without verification, we train the nCBF with a fixed data set and stop training after 200 epochs. We then examine the satisfaction of one of the CBF conditions with a denser testing dataset. The 0-superlevel set of the trained NN is shown in blue in the left Figure above. The orange area indicates the testing data points that violate the condition. We resume the training with the same dataset and use BBVT to augment the training dataset with CEs every k epochs until the verifier returns satisfaction. The middle Figure shows the distribution of the CEs after the first verification loop. As we augment the dataset, the verifier returns satisfaction after 240 epochs, see the right Figure.

To highlight the efficacy of BBVT, we evaluate the training time, verification time, and the ratio of violation areas for our framework and baseline methods. We show that our framework efficiently synthesizes an nCBF which renders a larger safe set than state-of-the-art methods without requiring an initial guess. The datailed results can be found in the thesis and paper.

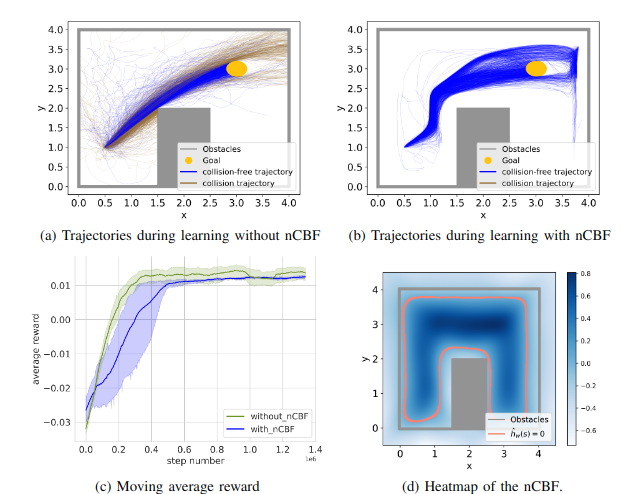
We use RL to address a 2D navigation task. We use the learned nCBF to filter the actions generated by the RL agent to ensure safety. We note that, theoretically, this controller guarantees safety with infinite control frequency. However, a continuous con- troller is not possible to implement on discrete control units. This limits the safety guarantees we may provide. How to address the gap between continuous controllers and their discrete implementations remains an open question. Figure a below shows all trajectories performed during the nominal RL training without the nCBF. We can see that several trajectories collide with the obstacles. When applying the nCBF as a safety filter there are no unsafe trajectories, as it can be seen in Figure b. However, we observe that the average reward with nCBF is larger than for nominal RL without nCBF in the very early stage but has a slower growth rate and converges to a lower reward level compared with nominal RL. The reason is that nCBF provides prior knowledge about the environment and the agent could avoid exploring unsafe regions in the early stage and gain a higher reward than nominal RL. However, the forward invari- ant set is still suboptimal, which means only a suboptimal policy is learned and exploration is restricted. Nevertheless, we believe that provided safety guarantees are beneficial in safety-critical applications.

Conclusions

This thesis presented a framework that simultaneously synthesizes and verifies continuous Neural Control Barrier Functions (nCBFs). To this end, we leveraged bound propagation techniques and the Branch-and-Bound scheme to efficiently verify neural networks as Control Barrier Functions (CBFs) in the continuous state space. In experiments, we showed that our framework efficiently synthesizes an nCBF which renders a larger safe set than state-of-the-art methods without requiring an initial guess. Since the memory requirements and computation time of the Branch-and-Bound Verification scheme increase exponentially with the system dimension, in future work, we may address the scalability of our framework.