Embedded Hierarchical MPC for Autonomous Navigation

Dennis Benders¹ Johannes Köhler² Thijs Niesten¹ Robert Babuška^1,3 Javier Alonso-Mora¹ Laura Ferranti¹

¹TU Delft ²ETH Zürich ³CTU Prague

Teaser

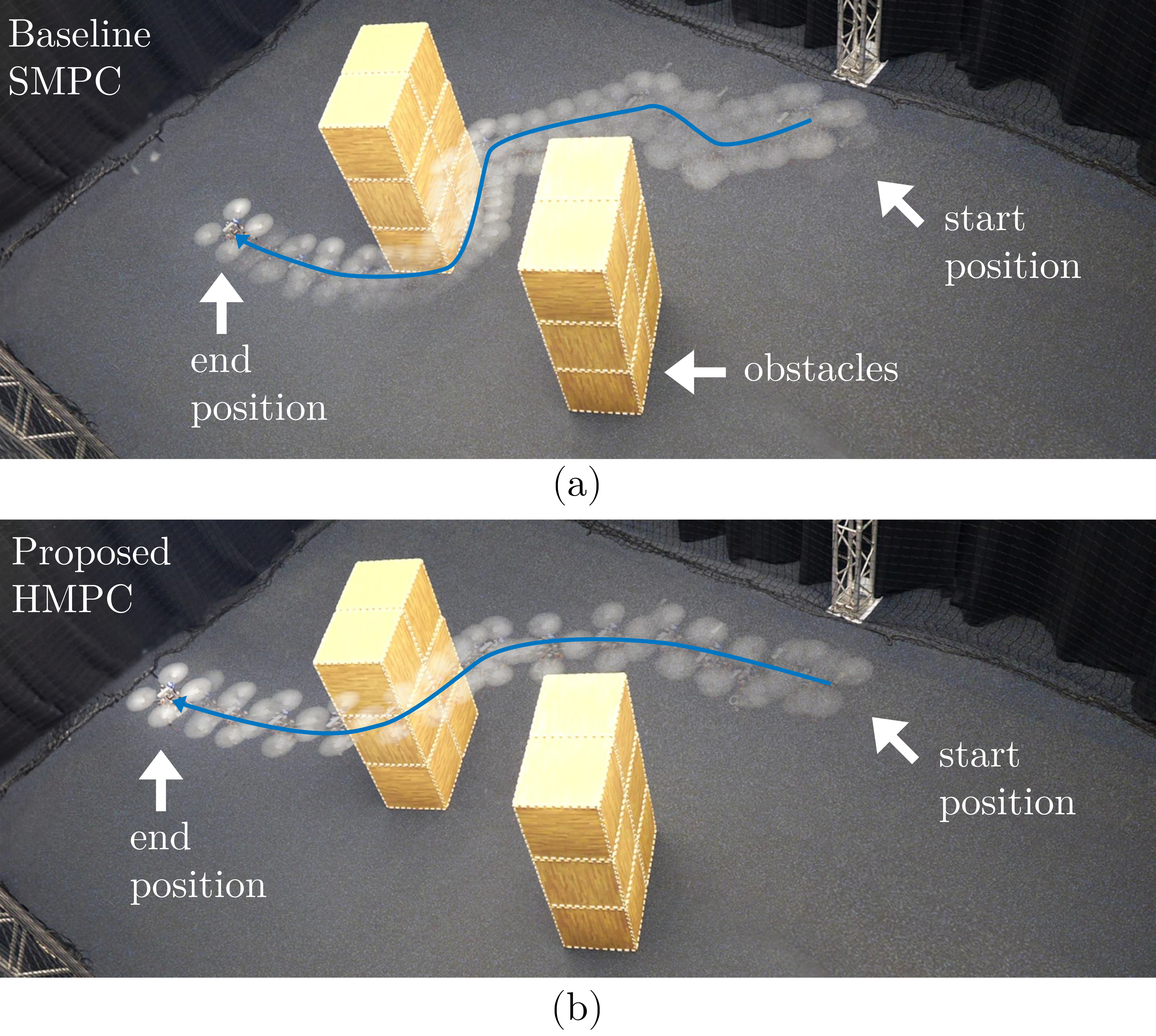
The closed-loop trajectory of (a) the baseline single-layer MPC (SMPC) scheme and (b) the proposed HMPC scheme. Whereas SMPC solves the planning and tracking tasks in a single-layer formulation, HMPC decouples the tasks using a planning MPC and a tracking MPC that use the same nonlinear model but run at different frequencies. SMPC uses the same nonlinear model as PMPC and TMPC and is sampled at the same rate as TMPC to ensure reliable operation. Both schemes fly from start to goal position and avoid the obstacles. Compared to SMPC, HMPC has a significantly longer planning horizon, given the limited computational resources on the onboard computer, and does not have to balance planning and tracking tasks. Therefore, HMPC reaches the goal faster, is less sensitive to model mismatch, and maintains altitude better than SMPC.

Abstract

To efficiently deploy robotic systems in society, mobile robots must move autonomously and safely through complex environments. Nonlinear model predictive control (MPC) methods provide a natural way to find a dynamically feasible trajectory through the environment without colliding with nearby obstacles. However, the limited computation power available on typical embedded robotic systems, such as quadrotors, poses a challenge to running MPC in real time, including its most expensive tasks: constraints generation and optimization. To address this problem, we propose a novel hierarchical MPC (HMPC) scheme that consists of a planning and a tracking layer. The planner constructs a trajectory with a long prediction horizon at a slow rate, while the tracker ensures trajectory tracking at a relatively fast rate. We prove that the proposed framework avoids collisions and is recursively feasible. Furthermore, we demonstrate its effectiveness in simulations and lab experiments with a quadrotor that needs to reach a goal position in a complex static environment. The code is efficiently implemented on the quadrotor's embedded computer to ensure real-time feasibility. Compared to a state-of-the-art single-layer MPC formulation, this allows us to increase the planning horizon by a factor of 5, which results in significantly better performance.

Embedded HMPC

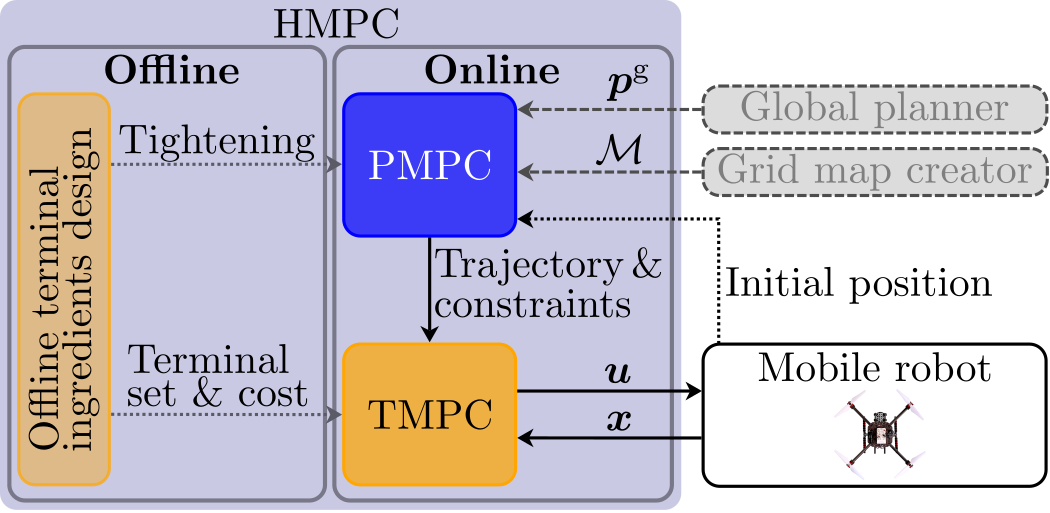
The goal is to plan and track a collision-free trajectory towards goal position $\boldsymbol{p}^\mathrm{g}$ given the initial position of the mobile robot and grid map $\mathcal{M}$ of the environment.

Below, we summarize some important properties of the proposed HMPC scheme. Please refer to Section V in the paper for more details.

In offline phase, we compute the terminal ingredients of the tracking MPC (TMPC). These ingredients include terminal cost matrix $P$ and feedback control gain $K$ that renders a sublevel set of the terminal cost function invariant. This sublevel set is the terminal set and its size is given by terminal set scaling $\alpha$. Furthermore, we compute Lipschitz constants $\boldsymbol{c}^\mathrm{s}$ and $c^\mathrm{o}$ for the planning MPC (PMPC), such that the TMPC satisfies the original system and obstacle avoidance constraints if these constraints are tightened by a multiplication of the tightening constants and $\alpha$ in the PMPC formulation.
See Algorithm 1 in the paper for more details on the offline design.

In online phase, we:

generate obstacle avoidance constraints using the I-DecompUtil method explained below;
optimize a dynamically feasible and collision-free trajectory by solving the PMPC problem with a goal-oriented objective function and tightened constraints. See Section III in the paper for more details on the properties that the trajectory needs to satisfy;
communicate the optimized trajectory and corresponding obstacle avoidance constraints from PMPC to TMPC via the specific interconnection scheme explained next;
track the trajectory and satisfy the constraints by solving the TMPC problem with reference tracking objective and terminal set constraint.

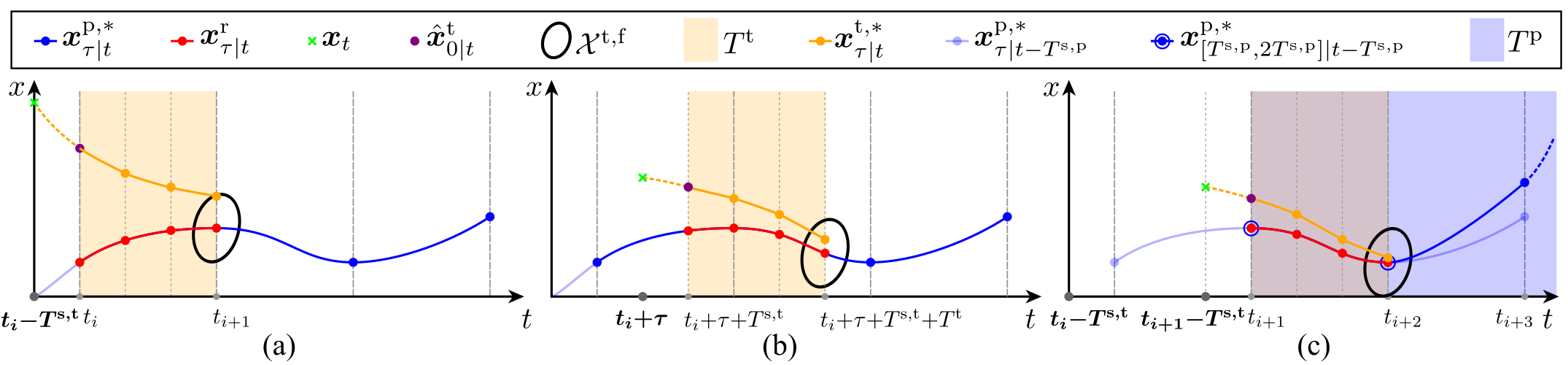
See Algorithm 2 in the paper for more details on the online design.

This following figure illustrates the interconnection scheme between PMPC and TMPC using a 1D state trajectory example:

At time $t_i-T^{\mathrm{s},\mathrm{t}}$, the TMPC optimizes a trajectory (orange) over horizon $T^\mathrm{t}$ starting from forward-simulated state $\hat{\boldsymbol{x}}_{0|t_i}^t$ (purple), which is the model response when applying $\boldsymbol{u}_{[0,T^{\mathrm{s},\mathrm{t}}]|t_i-T^{\mathrm{s},\mathrm{t}}}^{\mathrm{t},*}$ starting from current state $\boldsymbol{x}_{t_i-T^{\mathrm{s},\mathrm{t}}}$ (green). The trajectory ends in terminal set $\mathcal{X}^\mathrm{f,t}$ around the reference trajectory $\boldsymbol{x}_{\tau|t_i}^\mathrm{r}$ (red) that becomes valid at $t_i$. $\boldsymbol{x}_{\tau|t_i}^\mathrm{r}$ is the sub-sampled version of reference plan $\boldsymbol{x}_{\tau|t_i}^{\mathrm{p},*}$ (blue).
In this example, the TMPC executes 2 more times ($\tau \in \{0,T^{\mathrm{s},\mathrm{t}}\}$) until the next reference trajectory becomes valid, thereby getting closer to the reference.
At time $t_{i+1}-T^{\mathrm{s},\mathrm{t}}$, the TMPC starts optimizing a trajectory based on a new reference plan $\boldsymbol{x}_{\tau|t_{i+1}}^{\mathrm{p},*}$ that becomes valid at $t_{i+1}$. This reference plan is optimized by the PMPC starting at time $t_i - T^{\mathrm{s},\mathrm{t}}$.

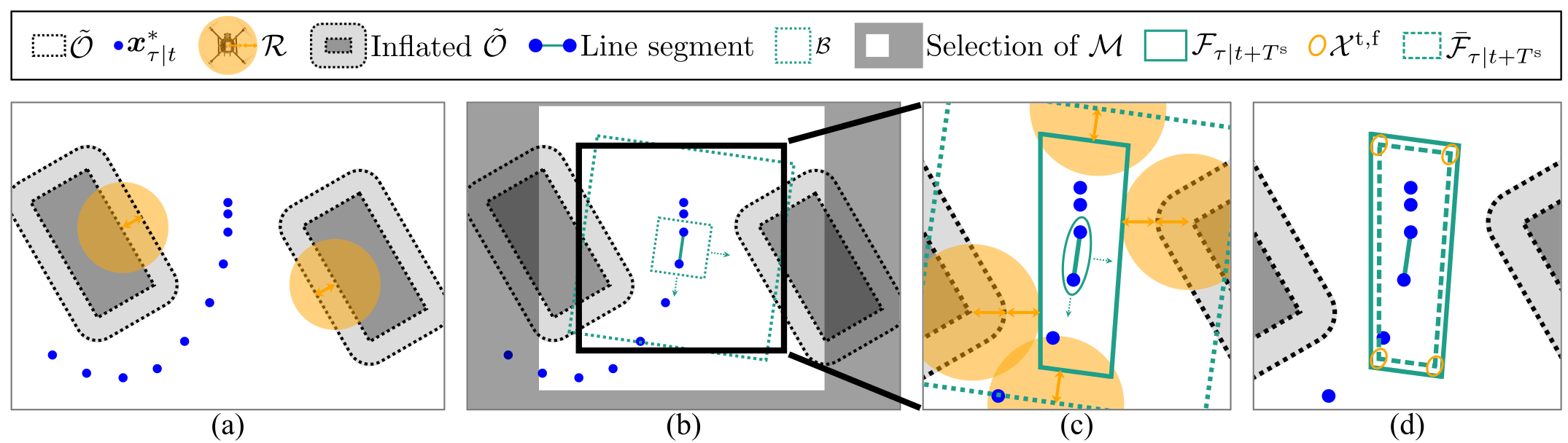
Obstacle avoidance generation using I-DecompUtil

The figure below gives a 2D visualization of map pre-processing and I-DecompUtil, given occupied grid cells $\tilde{\mathcal{O}}$ and the last optimized plan $\boldsymbol{x}_{\tau|t}^*$:

The obstacles are inflated by half of the robot radius (orange arrows).
To construct the obstacle avoidance constraints around a specific line segment, first, a subset of the grid map $\mathcal{M}$ is selected such that the bounding box $\mathcal{B}$ with any orientation fits in this subset.
The obstacle avoidance constraints $\mathcal{F}_{\tau|t+T^\mathrm{s,p}}$ are constructed according to the DecompUtil method^[1] by growing an ellipsoid around the line segment, creating the tangential lines and clipping them to $\mathcal{B}$. Furthermore, $\mathcal{F}_{\tau|t+T^\mathrm{s,p}}$ are tightened by the other half of the robot radius, such that the robot does not collide with the obstacles if its center satisfies $\mathcal{F}_{\tau|t+T^\mathrm{s,p}}$.
The tightened obstacle avoidance constraints $\bar{\mathcal{F}}_{\tau|t+T^\mathrm{s,p}}$ are constructed by tightening $\mathcal{F}_{\tau|t+T^\mathrm{s,p}}$ with $c^\mathrm{o} \alpha$, visualized using terminal set $\mathcal{X}^\mathrm{f,t}$ in this figure.

Note that (b)-(d) are repeated for all line segments.

Please refer to Section IV in the paper for more details on the design of the obstacle avoidance generation.

Want to know how to efficiently implement this method on an embedded computer? Checkout Section VI-B1 in the paper!

Results

We demonstrate two types of results:

HMPC properties.
Performance comparison with a baseline single-layer MPC (SMPC) scheme.

Please refer to Section VI in the paper for more details on the results.

HMPC properties

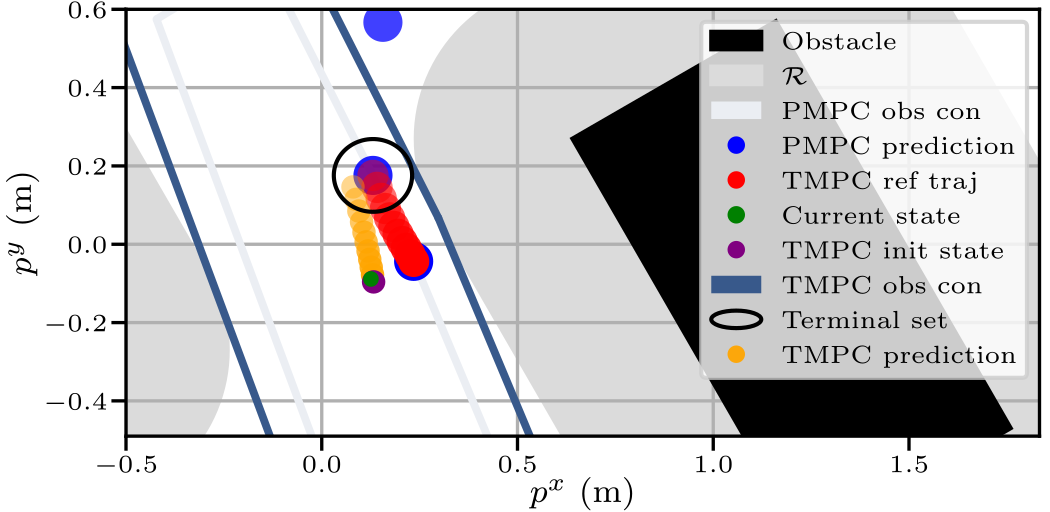
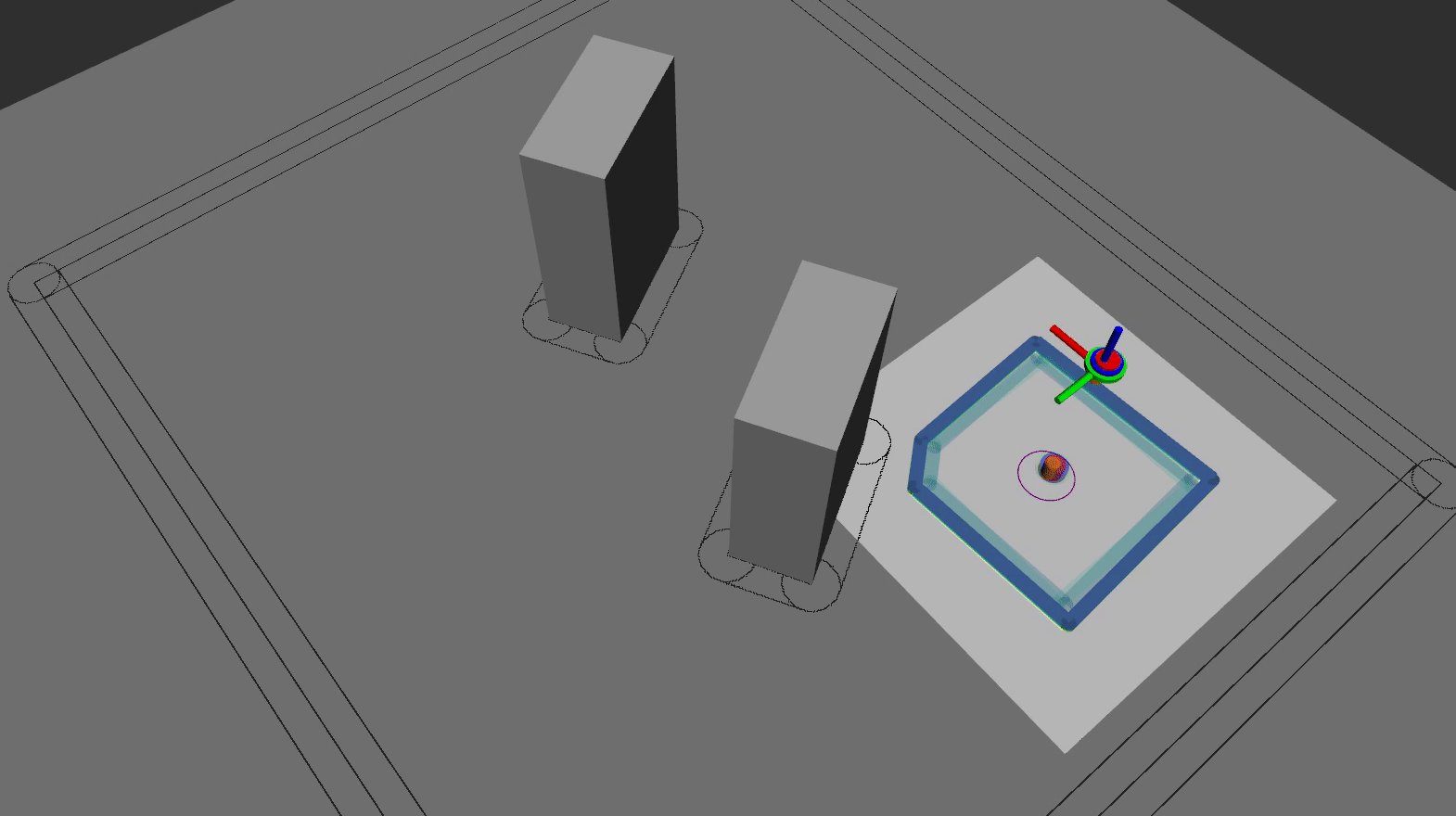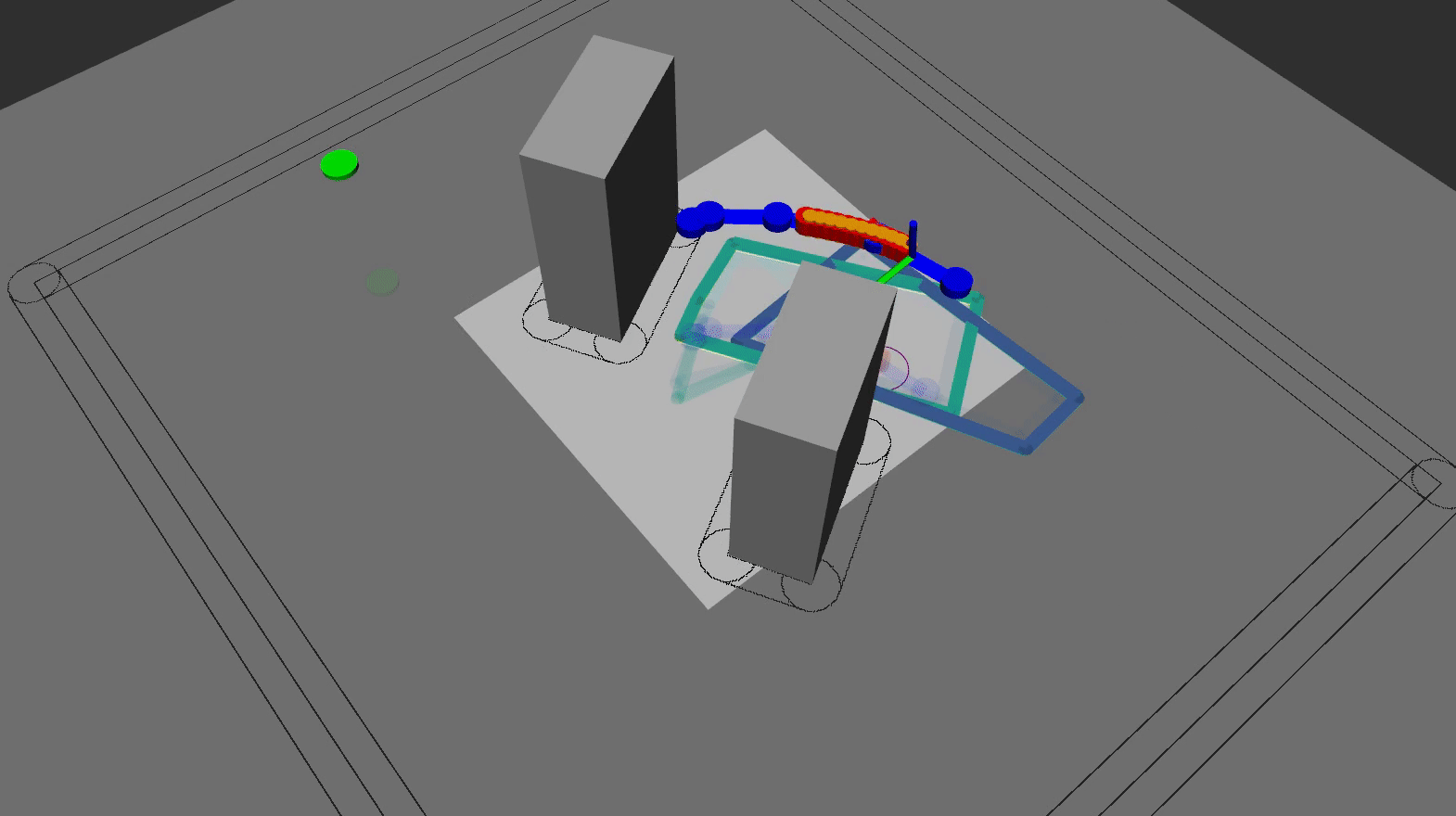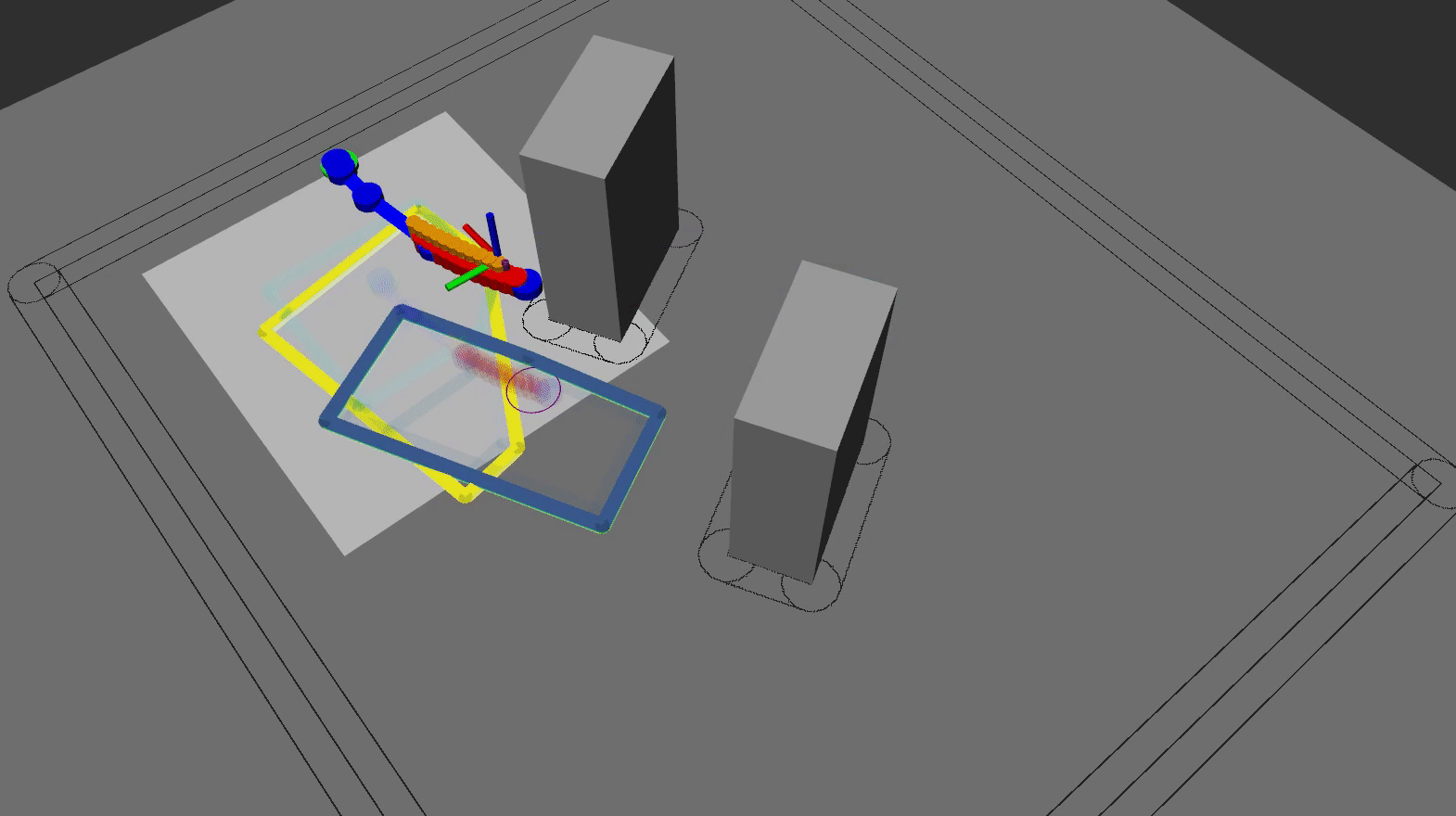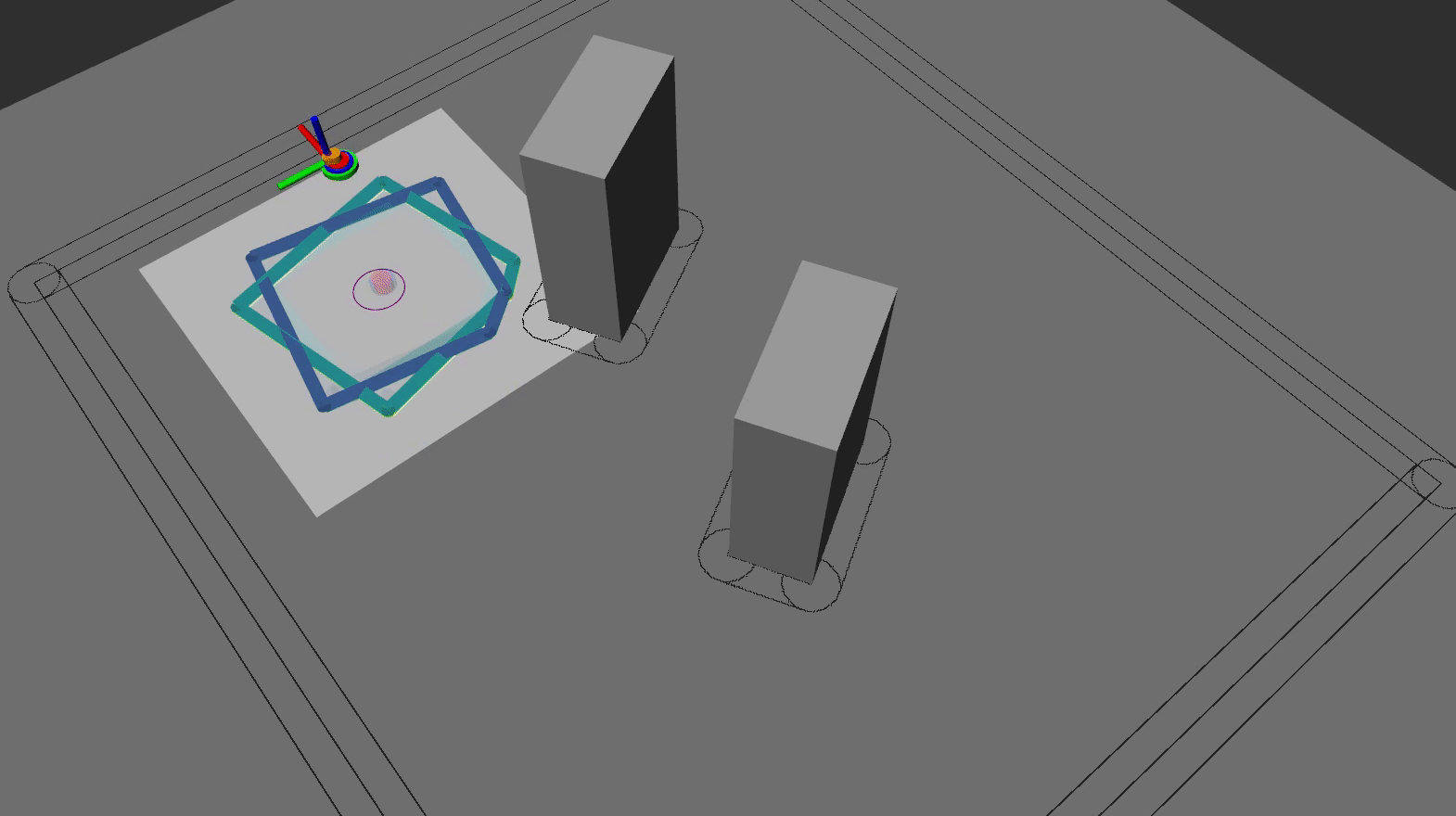
This figure shows a specific snapshot of the TMPC prediction starting from forward-simulated state TMPC init state and ending in the terminal set, given the obstacles, their collision region based on robot region $\mathcal{R}$, reference plan PMPC prediction and corresponding reference trajectory TMPC ref traj, and obstacle avoidance constraints PMPC obs con. Note that the PMPC obstacle avoidance constraints are tightened with respect to TMPC obstacle avoidance constraints TMPC obs con, and Current state and forward-simulated state do not overlap, showing the presence of model mismatch.

The animation below shows the the RViZ visualization of the quadrotor flying in the lab using the HMPC scheme:

In summary, based on all HMPC results, we conclude that:

HMPC is able to efficiently navigate from start to goal position while avoiding the obstacles;
HMPC runs in real time on the quadrotor's embedded computer;
In the absence of model mismatch, HMPC guarantees obstacle avoidance and recursive feasibility;
In the presence of model mismatch, HMPC is empirically shown to avoid obstacles and run without infeasibility of both PMPC and TMPC.

Performance comparison with SMPC

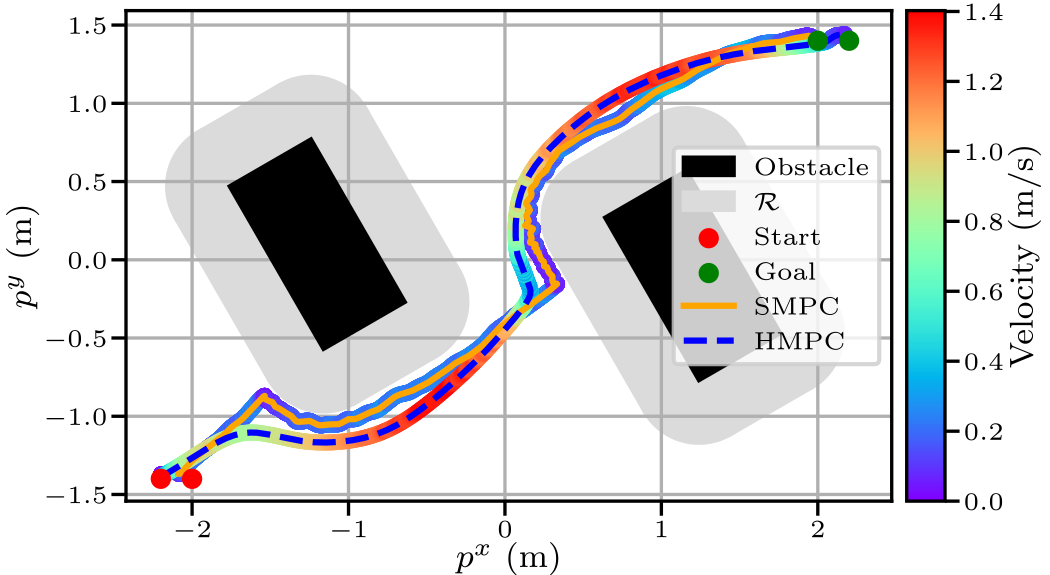
We compared the performance of the proposed HMPC scheme with SMPC in simulations and lab experiments. The figure on the right shows the 2D closed-loop SMPC and HMPC trajectories with associated velocities in lab experiments. HMPC has a longer planning horizon and results in a smoother trajectory reaching the goal in 8.1 s versus 35.1 s for SMPC. Note that the start and goal positions for SMPC are closer. Otherwise, SMPC cannot find a way around the first encountered obstacle.

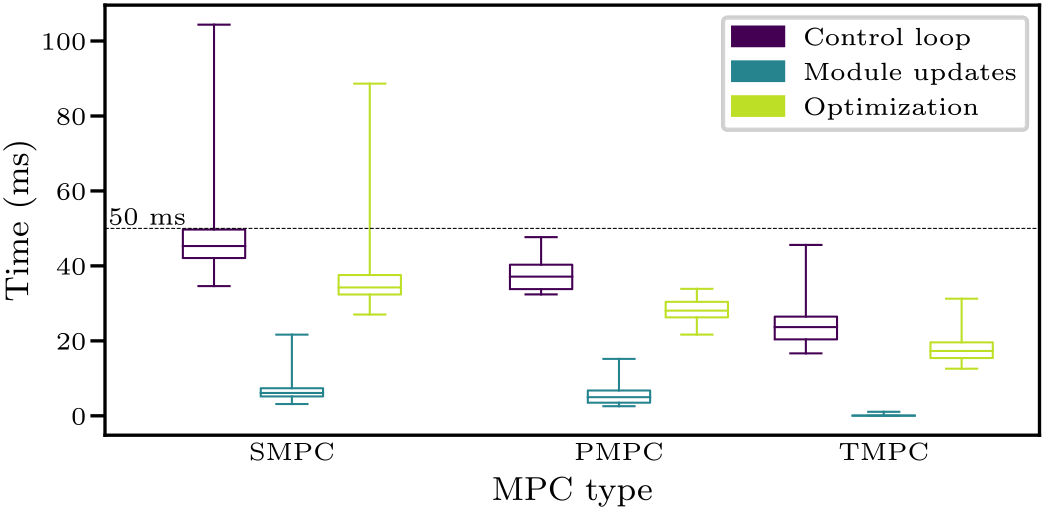
The main reason to use HMPC on an embedded computer is its computational efficiency. The figure on the right shows a boxplot with overall execution times for SMPC and HMPC (Control loop) and its most important parts: Module updates and Optimization. The maximum control loop execution time is 50 ms for real-time feasibility of SMPC and TMPC and 500 ms for PMPC. Note that Module updates includes constraints generation and loading new cost function terms, and is low compared to the optimization time. Since the TMPC receives the constraints from the PMPC, its Module updates computation time is even lower. Optimization is the time between calling the solver and obtaining the solution. SMPC contains several control loop cycles exceeding its real-time limit, whereas PMPC and TMPC always finish on time.

In summary, based on all HMPC and SMPC results, we conclude that, compared to SMPC, HMPC:

is computationally more effecient;
reaches the goal faster;
is less sensitive to model mismatch;
does not require constraints softening to ensure feasibility.

A note on tuning hyperparameters

To run the HMPC scheme, we need to tune several hyperparameters. The most important ones are:

MPC discretization time $T^\mathrm{s}$;
MPC horizon length $T$;
MPC objective weights;
Terminal set scaling $\alpha$;
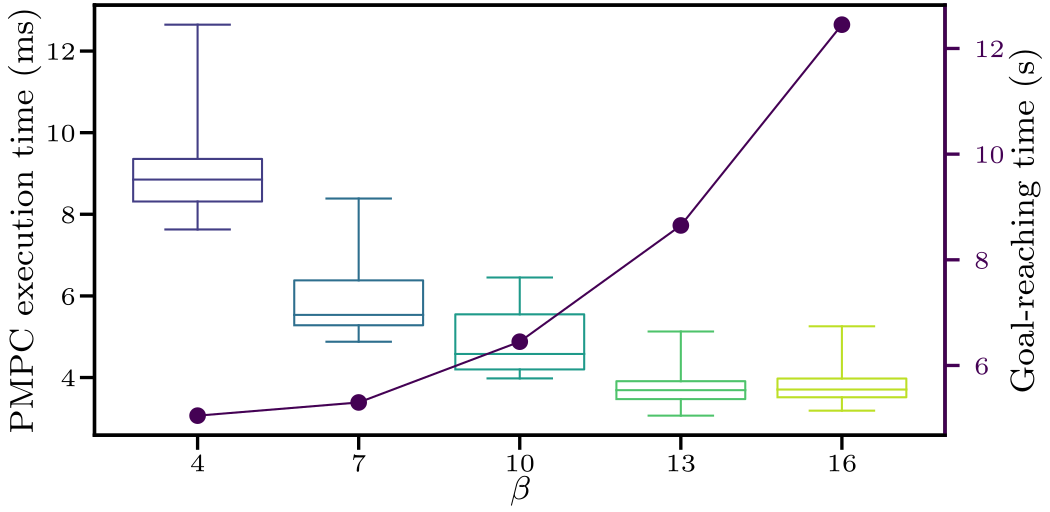
Ratio between sampling times of PMPC and TMPC $\beta$.

The TMPC discretization time $T^\mathrm{s,t}$ is chosen small enough to ensure accurate control and large enough to solve the MPC problem with a reasonable horizon $T^\mathrm{t}$ in real time on the embedded computer. We choose the PMPC discretization time $T^\mathrm{s,p}$ using the ratio $\beta=\frac{T^\mathrm{s,p}}{T^\mathrm{s,t}}$. As shown in the figure below, $\beta$ gives a trade-off between the PMPC execution time and the goal-reaching time. From this figure we can conclude that $\beta=10$ is a reasonable value to choose. From there, we choose the PMPC horizon length $T^\mathrm{p}$ to be short enough to ensure real-time feasibility and long enough to compute a reasonable trajectory around the obstacles towards the goal. The input weights in both TMPC and PMPC are chosen sufficiently large to ensure stability of the closed-loop system, and the goal and state weights are chosen sufficiently large to ensure that the system reaches the goal and accurately tracks the reference trajectory in the case of PMPC and TMPC, respectively. Finally, the terminal set scaling $\alpha$ is chosen large enough to ensure TMPC feasibility and small enough to optimize a trajectory with limited conservativeness in the PMPC.

There is more!

HMPC has more capabilities. Interested? Check out the YouTube video and the code!
Special care has been taken to construct the repository according to the guidelines presented in recent work^[2] to enhance reproducibility.

Research platform

The platform used in the lab experiments of this work is based on the NXP HoverGames kit. On top of this kit, we have added an NVIDIA Jetson Xavier NX embedded computer that runs all code.

References

S. Liu, M. Watterson, K. Mohta, K. Sun, S. Bhattacharya, C. J. Taylor, and V. Kumar, “Planning dynamically feasible trajectories for quadrotors using safe flight corridors in 3-d complex environments,” IEEE Robotics and Automation Letters, vol. 2, no. 3, pp. 1688–1695, 2017.
E. Cervera, “Try to start it! the challenge of reusing code in robotics research,” IEEE Robotics and Automation Letters, vol. 4, no. 1, pp. 49–56, 2018.

Embedded Hierarchical MPC for Autonomous Navigation
Dennis Benders, Johannes Köhler, Thijs Niesten, Robert Babuška, Javier Alonso-Mora, Laura Ferranti. In IEEE Transactions on Robotics (T-RO), 2025.

abstract IEEE Xplore arXiv code web video

To efficiently deploy robotic systems in society, mobile robots must move autonomously and safely through complex environments. Nonlinear model predictive control (MPC) methods provide a natural way to find a dynamically feasible trajectory through the environment without colliding with nearby obstacles. However, the limited computation power available on typical embedded robotic systems, such as quadrotors, poses a challenge to running MPC in real time, including its most expensive tasks: constraints generation and optimization. To address this problem, we propose a novel hierarchical MPC scheme that consists of a planning and a tracking layer. The planner constructs a trajectory with a long prediction horizon at a slow rate, while the tracker ensures trajectory tracking at a relatively fast rate. We prove that the proposed framework avoids collisions and is recursively feasible. Furthermore, we demonstrate its effectiveness in simulations and lab experiments with a quadrotor that needs to reach a goal position in a complex static environment. The code is efficiently implemented on the quadrotor's embedded computer to ensure real-time feasibility. Compared to a state-of-the-art single-layer MPC formulation, this allows us to increase the planning horizon by a factor of 5, which results in significantly better performance.

Where to Look Next: Learning Viewpoint Recommendations for Informative Trajectory Planning
M. Lodel, B. Brito, A. Serra-Gomez, L. Ferranti, R. Babuska, J. Alonso-Mora. In Proc. IEEE Int. Conf. on Robotics and Automation (ICRA), 2022.

abstract arxiv pdf video

Search missions require motion planning and navigation methods for information gathering that continuously replan based on new observations of the robot's surroundings. Current methods for information gathering, such as Monte Carlo Tree Search, are capable of reasoning over long horizons, but they are computationally expensive. An alternative for fast online execution is to train, offline, an information gathering policy, which indirectly reasons about the information value of new observations. However, these policies lack safety guarantees and do not account for the robot dynamics. To overcome these limitations we train an information-aware policy via deep reinforcement learning, that guides a receding-horizon trajectory optimization planner. In particular, the policy continuously recommends a reference viewpoint to the local planner, such that the resulting dynamically feasible and collision-free trajectories lead to observations that maximize the information gain and reduce the uncertainty about the environment. In simulation tests in previously unseen environments, our method consistently outperforms greedy next-best-view policies and achieves competitive performance compared to Monte Carlo Tree Search, in terms of information gains and coverage time, with a reduction in execution time by three orders of magnitude.

Learning Mixed Strategies in Trajectory Games
L. Peters, D. Fridovich-Keil, L. Ferranti, J. Alonso-Mora, F. Laine. In , Proc. of Robotics: Science and Systems (RSS), 2022.

abstract web pdf video

In multi-agent settings, game theory is a natural framework for describing the strategic interactions of agents whose objectives depend upon one another’s behavior. Trajectory games capture these complex effects by design. In competitive settings, this makes them a more faithful interaction model than traditional “predict then plan” approaches. However, current game-theoretic planning methods have important limitations. In this work, we propose two main contributions. First, we introduce an offline training phase which reduces the online computational burden of solving trajectory games. Second, we formulate a lifted game which allows players to optimize multiple candidate trajectories in unison and thereby construct more competitive “mixed” strategies. We validate our approach on a number of experiments using the pursuit-evasion game “tag.”

Back to Publications