Game-Theoretic Motion Planning for Multi-Agent Interaction

project image

People

Lasse Peters - PhD candidate
Prof. Laura Ferranti
Prof. Javier Alonso-Mora

Funding

This project is funded in part by the National Police (Politie) of the Netherlands.

More Links
Code

About the Project

In order for robots to be helpful companions in our everyday lives, they must be able to operate outside of cages, alongside humans and other robots. This achievement would allow to deploy robots in a much greater set of applications than the ones that we seeing today with opportunities ranging from from autonomous driving in urban dense urban traffic to automation of hospital logistics. A key requirement to achieve this goal is the problem of safe and efficient motion planning in interaction with other decision-making entities. This requirement poses a particular challenge when the robot cannot directly communicate with other agents. In such a scenario, it is of utmost importance that autonomous agents understand the effect of their actions on the decisions of others.

A principled mathematical framework for modeling such interaction of multiple agents over time is provided by the field of dynamic game theory. In this framework, agents are modeled as rational decision-making entities with potentially differing objective whose actions affect the evolution of the state of a shared environment. The flexibility of this framework allows to capture a wide range of aspects and challenges common to real-world interactions, including noncooperative behavior, bounded rationality, and dynamic evolution of potentially imperfect and incomplete information available to each player. When solved to a generalized equilibrium concept, these problems can not only account for interdependence of preference but also for interdependence of feasible actions, e.g., collision avoidance constraints. This vast modeling capacity makes dynamic game theory an attractive framework for autonomous planning in the presence of other agents.

The goal of this project is to push the state-of-the-art in motion planning for multi-agent interaction by combining game-theoretic approaches with learning-based techniques. Through this combination, we aim to develop algorithms that admit autonomous strategic decision-making in realis- tic real-world scenarios with limited computational resources.

Project Demonstrations

Funding & Partners

Auto-Encoding Bayesian Inverse Games
Xinjie Liu, Lasse Peters, Javier Alonso-Mora, Ufuk Topcu, David Fridovich-Keil. In 16th Workshop on the Algorithmic Foundations of Robotics (WAFR), 2024.

pdf web
When multiple agents interact in a common environment, each agent's actions impact others' future decisions, and noncooperative dynamic games naturally capture this coupling. In interactive motion planning, however, agents typically do not have access to a complete model of the game, e.g., due to unknown objectives of other players. Therefore, we consider the inverse game problem, in which some properties of the game are unknown a priori and must be inferred from observations. Existing maximum likelihood estimation (MLE) approaches to solve inverse games provide only point estimates of unknown parameters without quantifying uncertainty, and perform poorly when many parameter values explain the observed behavior. To address these limitations, we take a Bayesian perspective and construct posterior distributions of game parameters. To render inference tractable, we employ a variational autoencoder (VAE) with an embedded differentiable game solver. This structured VAE can be trained from an unlabeled dataset of observed interactions, naturally handles continuous, multi-modal distributions, and supports efficient sampling from the inferred posteriors without computing game solutions at runtime. Extensive evaluations in simulated driving scenarios demonstrate that the proposed approach successfully learns the prior and posterior game parameter distributions, provides more accurate objective estimates than MLE baselines, and facilitates safer and more efficient game-theoretic motion planning.

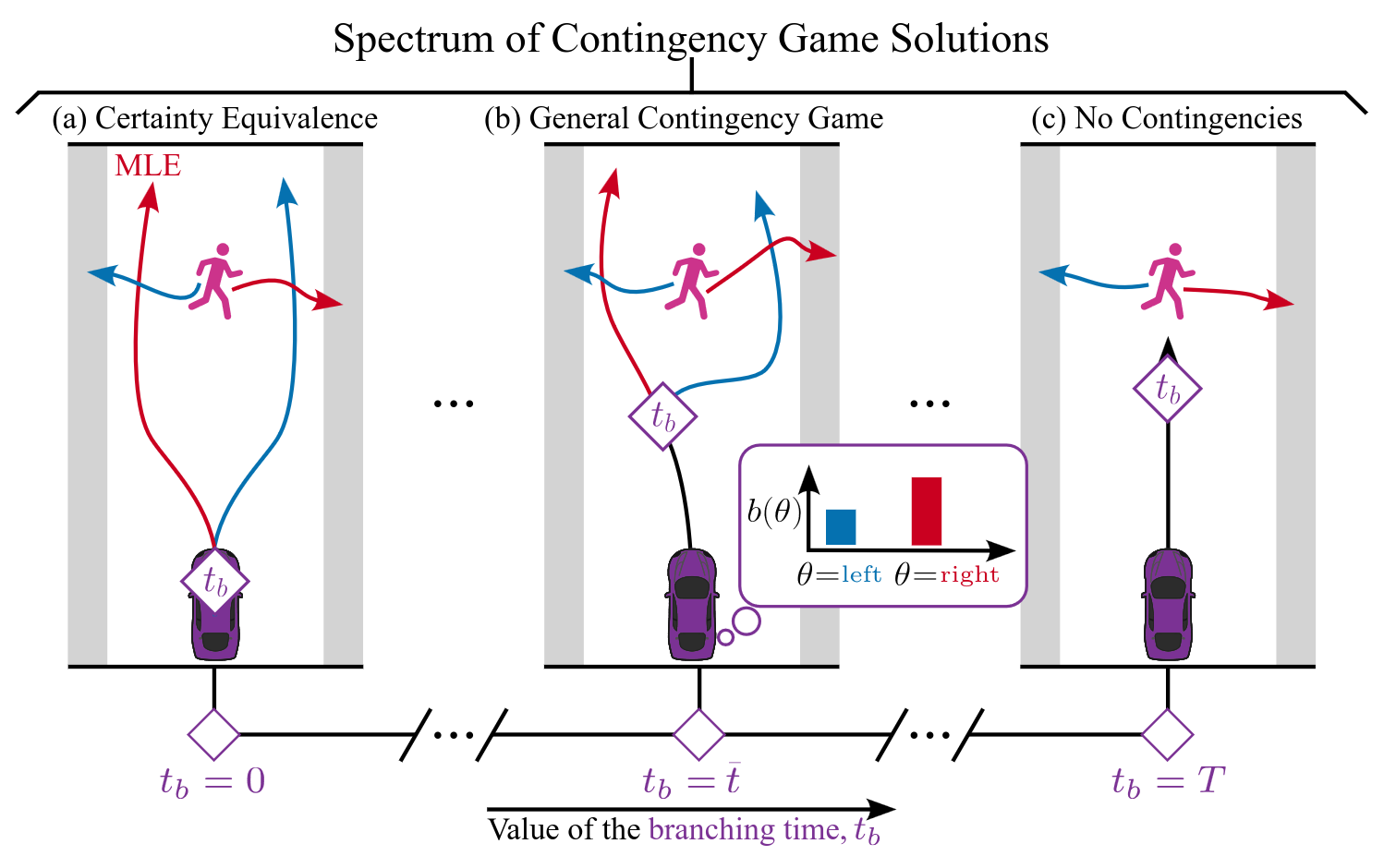
Contingency Games for Multi-Agent Interaction
Lasse Peters, Andrea Bajcsy, Chih-Yuan Chiu, David Fridovich-Keil, Forrest Laine, Laura Ferranti, Javier Alonso-Mora. In Robotics and Automation Letters (RA-L), 2024.

pdf web video
Contingency planning, wherein an agent generates a set of possible plans conditioned on the outcome of an uncertain event, is an increasingly popular way for robots to act under uncertainty. In this work we take a game-theoretic perspective on contingency planning, tailored to multi-agent scenarios in which a robot’s actions impact the decisions of other agents and vice versa. The resulting contingency game allows the robot to efficiently interact with other agents by generating strategic motion plans conditioned on multiple possible intents for other actors in the scene. Contingency games are parameterized via a scalar variable which represents a future time when intent uncertainty will be resolved. By estimating this parameter online, we construct a game-theoretic motion planner that adapts to changing beliefs while anticipating future certainty. We show that existing variants of game-theoretic planning under uncertainty are readily obtained as special cases of contingency games. Through a series of simulated autonomous driving scenarios, we demonstrate that contingency games close the gap between certainty-equivalent games that commit to a single hypothesis and non-contingent multi-hypothesis games that do not account for future uncertainty reduction.
paper image

Online and offline learning of player objectives from partial observations in dynamic games
L. Peters, V. Rubies-Royo, C. J. Tomlin, L. Ferranti, J. Alonso-Mora, C. Stachniss, D. Fridovich-Keil. In The International Journal of Robotics Research (IJRR), 2023.

pdf web
Robots deployed to the real world must be able to interact with other agents in their environment. Dynamic game theory provides a powerful mathematical framework for modeling scenarios in which agents have individual objectives and interactions evolve over time. However, a key limitation of such techniques is that they require a priori knowledge of all players’ objectives. In this work, we address this issue by proposing a novel method for learning players’ objectives in continuous dynamic games from noise-corrupted, partial state observations. Our approach learns objectives by coupling the estimation of unknown cost parameters of each player with inference of unobserved states and inputs through Nash equilibrium constraints. By coupling past state estimates with future state predictions, our approach is amenable to simultaneous online learning and prediction in receding horizon fashion. We demonstrate our method in several simulated traffic scenarios in which we recover players’ preferences, for, e.g. desired travel speed and collision-avoidance behavior. Results show that our method reliably estimates game-theoretic models from noise-corrupted data that closely matches ground-truth objectives, consistently outperforming state-of-the-art approaches.

Learning to Play Trajectory Games Against Opponents with Unknown Objectives
X. Liu, L. Peters, J. Alonso-Mora. In IEEE Robotics and Automation Letters (RA-L), 2023.

web pdf video
Many autonomous agents, such as intelligent ve- hicles, are inherently required to interact with one another. Game theory provides a natural mathematical tool for robot motion planning in such interactive settings. However, tractable algorithms for such problems usually rely on a strong assumption, namely that the objectives of all players in the scene are known. To make such tools applicable for ego-centric planning with only local information, we propose an adaptive model-predictive game solver, which jointly infers other players’ objectives online and computes a corresponding generalized Nash equilibrium (GNE) strategy. The adaptivity of our approach is enabled by a differentiable trajectory game solver whose gradient signal is used for maximum likelihood estimation (MLE) of opponents’ objectives. This differentiability of our pipeline facilitates direct integration with other differentiable elements, such as neural networks (NNs). Furthermore, in contrast to existing solvers for cost inference in games, our method handles not only partial state observations but also general inequality constraints. In two simulated traffic scenarios, we find superior performance of our approach over both existing game-theoretic methods and non- game-theoretic model-predictive control (MPC) approaches. We also demonstrate our approach’s real-time planning capabilities and robustness in two-player hardware experiments.

Learning Mixed Strategies in Trajectory Games
L. Peters, D. Fridovich-Keil, L. Ferranti, J. Alonso-Mora, F. Laine. In , Proc. of Robotics: Science and Systems (RSS), 2022.

web pdf video
In multi-agent settings, game theory is a natural framework for describing the strategic interactions of agents whose objectives depend upon one another’s behavior. Trajectory games capture these complex effects by design. In competitive settings, this makes them a more faithful interaction model than traditional “predict then plan” approaches. However, current game-theoretic planning methods have important limitations. In this work, we propose two main contributions. First, we introduce an offline training phase which reduces the online computational burden of solving trajectory games. Second, we formulate a lifted game which allows players to optimize multiple candidate trajectories in unison and thereby construct more competitive “mixed” strategies. We validate our approach on a number of experiments using the pursuit-evasion game “tag.”