Topology-Driven Parallel Trajectory Optimization in Dynamic Environments

Oscar de Groot1 Laura Ferranti1 Dariu M. Gavrila1 Javier Alonso-Mora1
1TU Delft
IEEE Xplore arXiv Code Video Related Publications

Regular MPC


Model Predictive Control (MPC) is a local planning method that usually locally optimizes a single trajectory. When its initial guess or current behavior is poor, it tends to get stuck in that behavior. This can lead to poor motion plans or even failure to find a motion plan.

Topology-Driven MPC


Topology-driven MPC (T-MPC++) is our new trajectory optimization framework that simultaneously computes multiple trajectories, each passing obstacles in a unique way. Our approach enables mobile robots to choose from multiple distinct locally optimal trajectories, significantly improving their ability to navigate dynamic, crowded environments.

Abstract

Ground robots navigating in complex, dynamic environments must compute collision-free trajectories to avoid obstacles safely and efficiently. Nonconvex optimization is a popular method to compute a trajectory in real-time. However, these methods often converge to locally optimal solutions and frequently switch between different local minima, leading to inefficient and unsafe robot motion. In this work, we propose a novel topology-driven trajectory optimization strategy for dynamic environments that plans multiple distinct evasive trajectories to enhance the robot's behavior and efficiency. A global planner iteratively generates trajectories in distinct homotopy classes. These trajectories are then optimized by local planners working in parallel. While each planner shares the same navigation objectives, they are locally constrained to a specific homotopy class, meaning each local planner attempts a different evasive maneuver. The robot then executes the feasible trajectory with the lowest cost in a receding horizon manner. We demonstrate, on a mobile robot navigating among pedestrians, that our approach leads to faster trajectories than existing planners.

Topology-Driven MPC


A schematic explanation of T-MPC. An environment with several obstacles and a robot is visualized in x, y, t (time in the upwards axis). Obstacle motion predictions are denoted with cylinders.

(Left) A guidance planner finds P = 4 trajectories (visualized with colored lines) from the robot initial position to one out of multiple goals. We filter trajectories on the way that they pass the obstacles using results from topology. As a result each of the guidance trajectories avoids obstacles differently.

(Middle) Each trajectory guides a local planner as initial guess and through a set of constraints that prevent the planner from changing its overtaking behavior. Four guidance trajectories and optimized trajectories (as occupied regions for each step) are visualized.

(Right) To decide on the trajectory to execute, the locally optimized trajectories are compared through their objective value the lowest cost trajectory (in red) is executed. This decision may take into account whether the robot was following the same behavior in the previous iteration.

We observed that adding a non-guided regular MPC in parallel to the guided planners further improves performance. In crowded environments, the regular MPC may occasionally find trajectories that the guidance planner does not find. By combining both strategies we eliminate key weaknesses in both planners. We refer to the combined planner as T-MPC++.

Simulation Results

Deterministic: Our results demonstrate that T-MPC++ allows mobile robots to navigate significantly faster through crowded environments than other planners. We compared against several planners (see the paper) in a corridor environment with a varying number of pedestrians following the social forces model. The figure shows the distribution of the task duration over 200 experiments for 4, 8 and 12 pedestrians. The vertical dashed line denotes the task duration without obstacles. Performance of TEB-Planner and LMPCC degrade in more crowded environments. Our previous work Guidance-MPCC can cause high (undesired) speeds leading to faster task durations than without obstacles. T-MPC++, slows down the least compared to the case without pedestrians without leading to collisions.

Uncertain: T-MPC++ can additionally handle different collision avoidance constraint formulations. For example, Chance-Constrained MPC (CC-MPC) considers Gaussian uncertainty in the future positions of obstacles. We showed that deploying T-MPC++ with CC-MPC constraints (referred to as TCC-MPC++) reduced the task duration and collisions compared to CC-MPC in isolation.

Real-World Experiments

We successfully applied T-MPC++ to navigate in a lab environment among 5 pedestrians, comparing it against LMPCC (i.e., regular MPC) and comparing TCC-MPC++ against CC-MPC. While the order of planners was randomized, participants unanimously preferred T-MPC++ and TCC-MPC++ over LMPCC and CC-MPC.

While the baseline planner regularly could not find a feasible trajectory or gets stuck in fast dangerous overtaking behaviors, T-MPC++ did not show these behaviors, which led to safer robot motion.

Code

Our implementation, including the simulation environments, is publicly available as a single VSCode containerized environment. The MPC and guidance planner are also available as stand-alone packages. Please see:

Topology-Driven Parallel Trajectory Optimization in Dynamic Environments
Oscar de Groot, Laura Ferranti, Dariu M. Gavrila, Javier Alonso-Mora. In IEEE Transaction on Robotics (T-RO), 2024.

pdf web video
Ground robots navigating in complex, dynamic environments must compute collision-free trajectories to avoid obstacles safely and efficiently. Nonconvex optimization is a popular method to compute a trajectory in real-time. However, these methods often converge to locally optimal solutions and frequently switch between different local minima, leading to inefficient and unsafe robot motion. In this work, we propose a novel topology-driven trajectory optimization strategy for dynamic environments that plans multiple distinct evasive trajectories to enhance the robot's behavior and efficiency. A global planner iteratively generates trajectories in distinct homotopy classes. These trajectories are then optimized by local planners working in parallel. While each planner shares the same navigation objectives, they are locally constrained to a specific homotopy class, meaning each local planner attempts a different evasive maneuver. The robot then executes the feasible trajectory with the lowest cost in a receding horizon manner. We demonstrate, on a mobile robot navigating among pedestrians, that our approach leads to faster trajectories than existing planners.
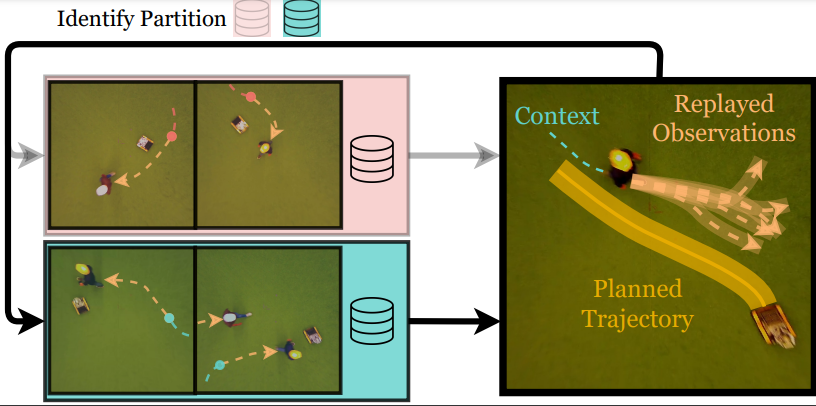
paper image

Probabilistic Motion Planning and Prediction via Partitioned Scenario Replay
Oscar de Groot, Anish Sridharan, Javier Alonso-Mora, Laura Ferranti. In IEEE Int. Conf. on Robotics and Automation (ICRA), 2024.

pdf video
Autonomous mobile robots require predictions of human motion to plan a safe trajectory that avoids them. Because human motion cannot be predicted exactly, future trajectories are typically inferred from real-world data via learning-based approximations. These approximations provide useful information on the pedestrian’s behavior, but may deviate from the data, which can lead to collisions during planning. In this work, we introduce a joint prediction and planning framework, Partitioned Scenario Replay (PSR), that stores and partitions previously observed human trajectories, referred to as scenarios. During planning, scenarios observed in similar situations are reintroduced (or replayed) as motion predictions. By sampling real data and by building on scenario optimization and predictive control, the planner provides probabilistic col- lision avoidance guarantees in the real-world. Relying on this guarantee to remain safe, PSR can incrementally improve its prediction and planning performance online. We demonstrate our approach on a mobile robot navigating around pedestrians.
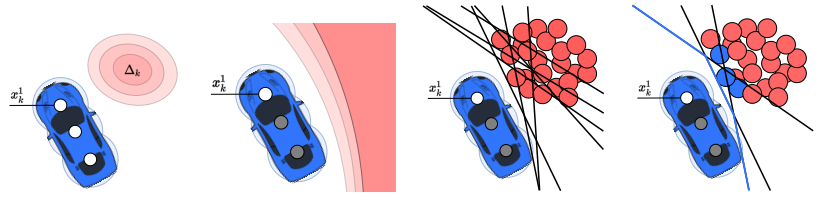
paper image

Probabilistic Risk Assessment for Chance-Constrained Collision Avoidance in Uncertain Dynamic Environments
Khaled A. Mustafa, Oscar de Groot, Xinwei Wang, Jens Kober, Javier Alonso-Mora. In IEEE International Conference on Robotics and Automation (ICRA), 2023.

pdf
Balancing safety and efficiency when planning in crowded scenarios with uncertain dynamics is challenging where it is imperative to accomplish the robot’s mission without incurring any safety violations. Typically, chance constraints are incorporated into the planning problem to provide probabilistic safety guarantees by imposing an upper bound on the collision probability of the planned trajectory. Yet, this results in overly conservative behavior on the grounds that the gap between the obtained risk and the specified upper limit is not explicitly restricted. To address this issue, we propose a real-time capable approach to quantify the risk associated with planned trajec- tories obtained from multiple probabilistic planners, running in parallel, with different upper bounds of the acceptable risk level. Based on the evaluated risk, the least conservative plan is selected provided that its associated risk is below a specified threshold. In such a way, the proposed approach provides probabilistic safety guarantees by attaining a closer bound to the specified risk, while being applicable to generic uncertainties of moving obstacles. We demonstrate the efficiency of our proposed approach, by improving the performance of a state- of-the-art probabilistic planner, in simulations and experiments using a mobile robot in an environment shared with humans.

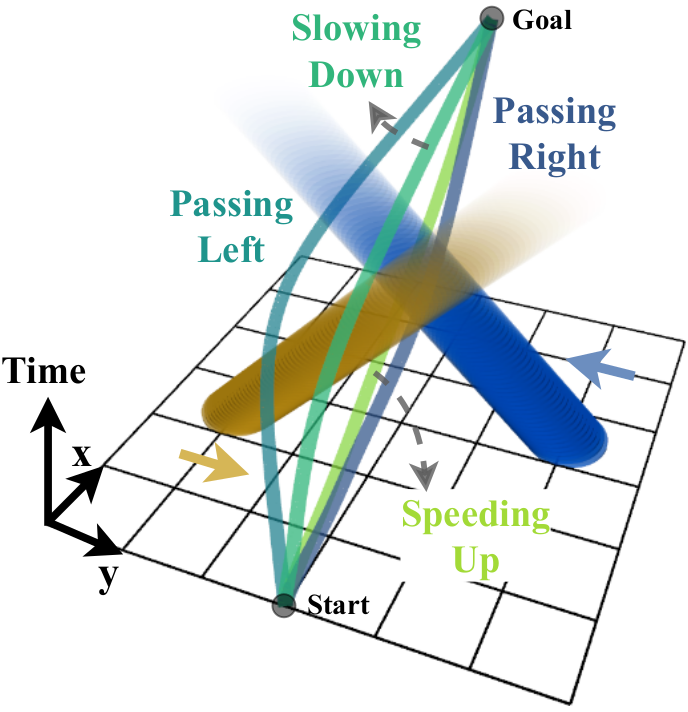
Globally Guided Trajectory Planning in Dynamic Environments
O. de Groot, L. Ferranti, D. Gavrila, J. Alonso-Mora. In IEEE Int. Conf. on Robotics and Automation (ICRA), 2023.

pdf video
Navigating mobile robots through environments shared with humans is challenging. From the perspective of the robot, humans are dynamic obstacles that must be avoided. These obstacles make the collision-free space nonconvex, which leads to two distinct passing behaviors per obstacle (passing left or right). For local planners, such as receding-horizon trajectory optimization, each behavior presents a local optimum in which the planner can get stuck. This may result in slow or unsafe motion even when a better plan exists. In this work, we identify trajectories for multiple locally optimal driving behaviors, by considering their topology. This identification is made consistent over successive iterations by propagating the topology information. The most suitable high-level trajectory guides a local optimization-based planner, resulting in fast and safe motion plans. We validate the proposed planner on a mobile robot in simulation and real-world experiments.
paper image

Scenario-Based Trajectory Optimization in Uncertain Dynamic Environments
O. de Groot, B. Brito, L. Ferranti, D. Gavrila, J. Alonso-Mora. In , IEEE Robotics and Automation Letters (RA-L), 2021.

arxiv pdf video
We present an optimization-based method to plan the motion of an autonomous robot under the uncertainties associated with dynamic obstacles, such as humans. Our method bounds the marginal risk of collisions at each point in time by incorporating chance constraints into the planning problem. This problem is not suitable for online optimization outright for arbitrary probability distributions. Hence, we sample from these chance constraints using an uncertainty model, to generate "scenarios", which translate the probabilistic constraints into deterministic ones. In practice, each scenario represents the collision constraint for a dynamic obstacle at the location of the sample. The number of theoretically required scenarios can be very large. Nevertheless, by exploiting the geometry of the workspace, we show how to prune most scenarios before optimization and we demonstrate how the reduced scenarios can still provide probabilistic guarantees on the safety of the motion plan. Since our approach is scenario based, we are able to handle arbitrary uncertainty distributions. We apply our method in a Model Predictive Contouring Control framework and demonstrate its benefits in simulations and experiments with a moving robot platform navigating among pedestrians, running in real-time.
paper image

Robust Collision Avoidance for Multiple Micro Aerial Vehicles Using Nonlinear Model Predictive Control
M. Kamel, J. Alonso-Mora, R. Siegwart, J. Nieto. In Proc. of the IEEE/RSJ Conf. on Robotics and Intelligent Systems (IROS), 2017.

publisher pdf video
When several Multirotor Micro Aerial Vehicles (MAVs) share the same airspace, reliable and robust collision avoidance is required. In this paper we address the problem of multi-MAV reactive collision avoidance. We employ a model-based controller to simultaneously track a reference trajectory and avoid collisions. Moreover, to achieve a higher degree of robustness, our method also accounts for the uncertainty of the state estimator and of the position and velocity of the other agents. The proposed approach is decentralized, does not require a collision-free reference trajectory and accounts for the full MAV dynamics. We validated our approach in simulation and experimentally with two MAV.
Back to Publications